Tutorial 2: Implementing perils in the GenMR digital template

Author: Arnaud Mignan, Mignan Risk Analytics GmbH
Version: 1.1.2
Last Updated: 2026-02-12
License: AGPL-3

Once a virtual environment has been generated (see previous tutorial), stochastic events are modelled to populate it. Table 1 lists the perils included in version 1.1.2 (the ones still missing to be included by June 2026).

Tab. 1. List of perils with identifiers (ID) according to Mignan (2024:tab.1.7).

ID	Peril	Peril type†	Source class	Event size	Intensity class	Intensity measure	Status‡
	NATURAL
AI	Asteroid impact	Primary	Point	Kinetic energy (kt)	Analytical	Overpressure (kPa)	✓
CS	Convertive storm	Primary (invisible\(^*\))	Area	Cloud top height (km)	Uniform	Cloud top height (km)	✓
Dr	Drought	Primary (invisible\(^*\))	Area	Duration (mon)	Threshold	Yes/no	✓
EQ	Earthquake	Primary	Line	Magnitude	Analytical	Peak ground acceleration (m/s\(^2\))	✓
FF	Fluvial flood	Secondary (to RS)	Point	Peak flow	Cellular automaton	Inundation depth (m)	✓
HW	Heatwave	Primary (invisible\(^*\))	Area	Duration (da)	Threshold	Inside/outside	✓
Li	Lightning	Secondary (to CS, invisible\(^*\))	Point	-	-	Yes/no	✓
LS	Landslide	Secondary (to RS)	Diffuse	Area (km\(^2\))	Cellular automaton	Thickness (m)	✓
PI	Pest infestation	Primary (invisible\(^*\))	Area	Mean norm. population size	Analytical	Normalised population size	✓
RS	Rainstorm	Primary (invisible\(^*\))	Area	Rain intensity (mm/hr)	Uniform	Rain intensity (mm/hr)	✓
SS	Storm surge	Secondary (to TC)	Line	Coastal surge height (m)	Threshold	Inundation depth (m)	✓
TC	Tropical cyclone	Primary	Track	Max. wind speed (m/s)	Analytical	Max. wind speed (m/s)	✓
To	Tornado	Primary	Line	Enhanced Fujita (EF) scale	Analytical	Max. wind speed (m/s)	✓
VE	Volcanic eruption	Primary	Point	Volume erupted (km\(^3\))	Analytical	Ash load (kPa)	✓
WF	Wildfire	Primary	Diffuse	Burnt area	Cellular automaton	Burnt/not burnt	✓
WS	Windstorm	Primary	Area	Max. wind speed (m/s)	Uniform	Max. wind speed (m/s)	✓
	TECHNOLOGICAL
BO	Blackout	Secondary (to dg)	Diffuse (network)				✗
Ex	Explosion (industrial)	Secondary (to dg)	Point	TNT mass (kt)	Analytical	Overpressure \(P\) (kPa)	✓
	SOCIO-ECONOMIC
BI	Business interruption						✗
Sf	Public service failure						✗
SU	Social unrest						✗

\(^*\) An event that does not cause any direct damage to buildings, at least in the present framework (following Mignan et al., 2014). Still implemented as triggering mechanism.
^† Most perils are considered primary perils in this tutorial for sake of simplicity. Several will be considered secondary perils in Tutorial 3.
^‡ Included in current version (✓), planned for v.1.1.2 (✗).

This tutorial is divided into two main sections. The first introduces the definition of peril sources, an event table (containing each event’s identifier and annual rate), and a corresponding catalogue of hazard-intensity footprints. The second section covers probabilistic risk assessment, in which damage and loss footprints are generated for each event identifier (Fig. 1) and risk metrics are calculated. Before beginning these sections, the digital-template environment created in the previous tutorial is loaded.

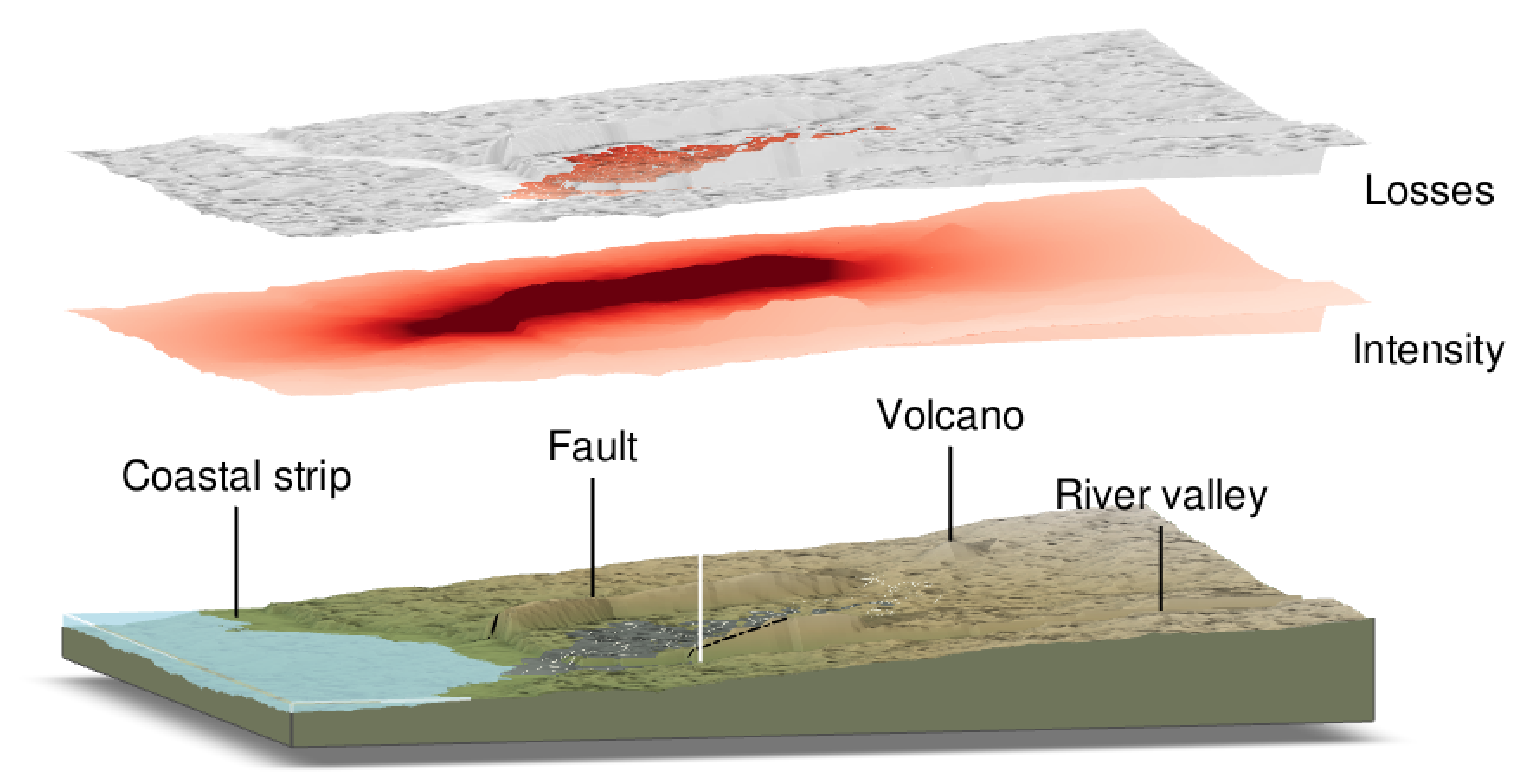
Fig. 1. One instance of the GenMR digital template (default parameterisation) with an example of event hazard intensity footprint and loss footprint (here for a large earthquake). Simulation rendered using Rayshader (Morgan-Wall, 2022).

import numpy as np
import pandas as pd
import copy
import matplotlib.pyplot as plt

import warnings 
warnings.filterwarnings('ignore')   # commented, try to remove all warnings

from GenMR import perils as GenMR_perils
from GenMR import environment as GenMR_env
from GenMR import utils as GenMR_utils


# load inputs (i.e., outputs from Tutorial 1)
file_src = 'src.pkl'
file_topoLayer = 'envLayer_topo.pkl'
file_atmoLayer = 'envLayer_atmo.pkl'
file_soilLayer = 'envLayer_soil.pkl'
file_urbLandLayer = 'envLayer_urbLand.pkl'
file_energyLayer = 'envLayer_energyCI.pkl'
src = GenMR_utils.load_pickle2class('/io/' + file_src)
grid = copy.copy(src.grid)
topoLayer = GenMR_utils.load_pickle2class('/io/' + file_topoLayer)
atmoLayer = GenMR_utils.load_pickle2class('/io/' + file_atmoLayer)
soilLayer = GenMR_utils.load_pickle2class('/io/' + file_soilLayer)
urbLandLayer = GenMR_utils.load_pickle2class('/io/' + file_urbLandLayer)
energyLayer = GenMR_utils.load_pickle2class('/io/' + file_energyLayer)

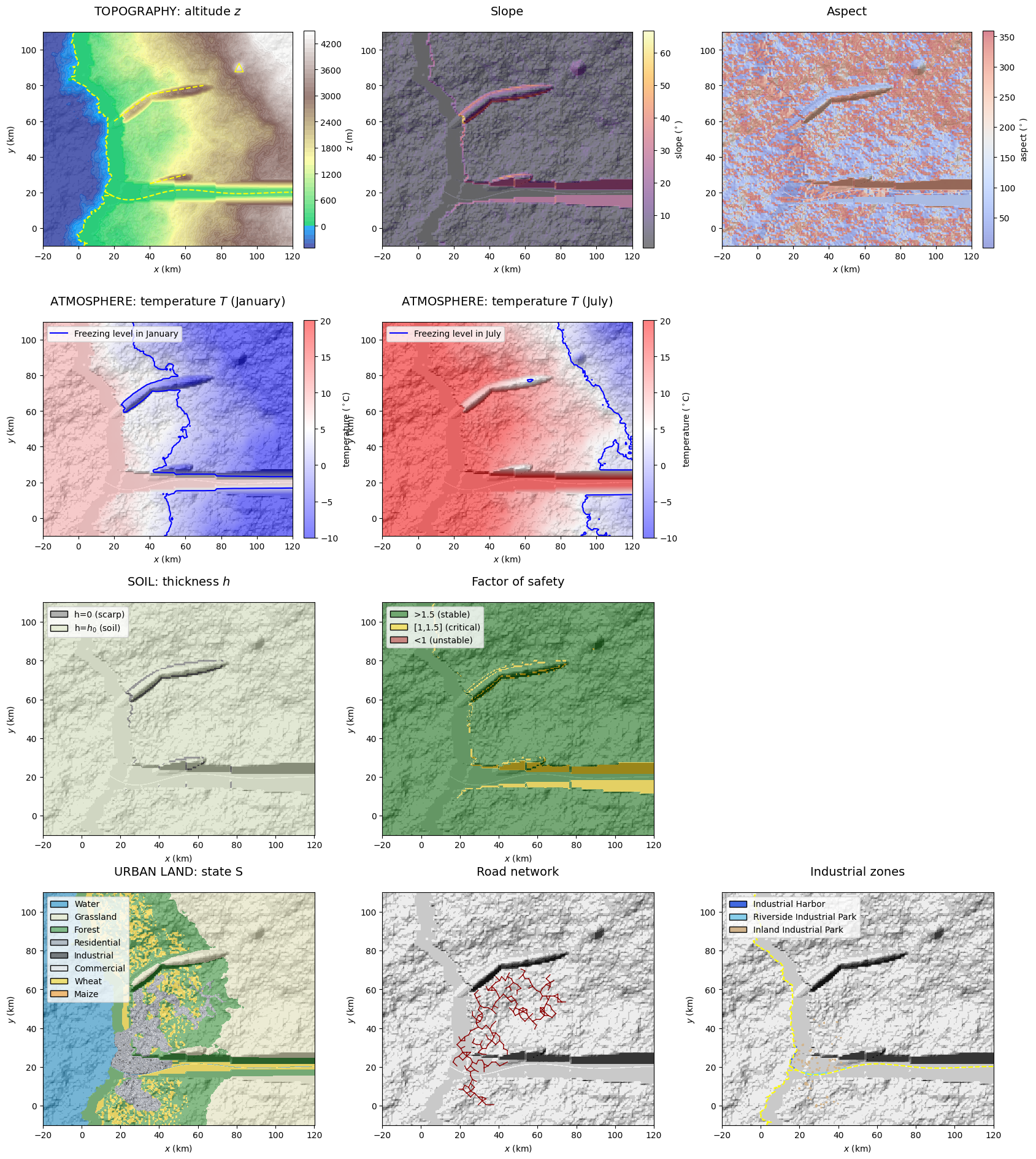
GenMR_env.plot_EnvLayers([topoLayer, atmoLayer, soilLayer, urbLandLayer], file_ext = 'jpg')

Note that the configuration of the digital template environment may be changed through Tutorial 1.

1. Stochastic event set

A list of stochastic events will be defined, consisting of both primary and secondary events. Because event interactions will be addressed in the next tutorial, only simple ad-hoc one-to-one interactions are introduced here to illustrate how secondary event footprints can be generated (e.g., a storm surge from a tropical cyclone or a landslide triggered by a rainstorm). Conditional probabilities of occurrence will be examined in Tutorial 3. In this tutorial, only primary events have assigned annual rates.

1.1. Peril source definition

Source characteristics for earthquakes, volcanic eruptions, and fluvial floods were defined in Tutorial 1, as some environmental layers depend directly on these perils. Additional peril sources are now introduced.

WARNING: Only perils listed in src.par['perils'] will be modelled. The following perils require long computation times (minutes to tens of minutes on the first run; subsequent runs load from cache): Ex, FF, HW, LS, WF

src.par['perils'] = ['AI','Dr','EQ','HW','PI','RS','TC','To','VE','WF','WS',  'CS',  'Ex','FF','Li','LS','SS']
                    # IMPORTANT: primary perils come first in src.par['perils']
                    # since 'CS' depends of 'To', must be listed after 'To' (i.e., CS=special peril)


src.par['rdm_seed'] = 42      # None or integer (for stochastic sources: AI, TC)
if 'To' not in src.par['perils'] and 'CS' in src.par['perils']:
    # convective storm char. depend on tornado char.
    src.par['perils'].remove('CS')

# define new perils ('EQ', 'FF', 'VE' already initiated in Tutorial 1)
## NATURAL ##
src.par['AI'] = {'object': 'impact', 'N': 10}     # random uniform asteroid impacts (point sources)
src.par['CS'] = {'object': 'supercell',           # as trigger of lightnings and tornadoes
                 'R_km': 10.,                     # path conditioned on tornado path (better constrained)
                 'dH_CS2tropopause_km': 1.,       # distance between cloud top and tropopause (km)
                 'lat_deg': grid.par['lat_deg'],
                 'vforward_m/s': 20.              # forward storm speed (m/s)
                }
src.par['CS']['S'] = atmoLayer.z_tropopause - src.par['CS']['dH_CS2tropopause_km'] # size as cloud top height (km)
src.par['Dr'] = {'object': 'soil',
                 'hw_th': .1,                     # 10% of normal soil water content hw_fc_m
                 'Si_mo': [3, 6, 9],              # Fixed event sizes (months) - for sake of illustration
                 'sigmaT_yearly': .55,            # Temp. std. dev. - value from Olonscheck et al. (2021)
                 'lat_deg': grid.par['lat_deg']}
src.par['HW'] = {'object': 'atmosphere',
                 'T_th': 35.,                     # Minimum temperature threshold (°C)
                 'Dt_da': 3.,                     # Minimum duration (days)
                 'Si_da': [7, 14, 30],            # Fixed event sizes (days) - for sake of illustration
                 'sigmaT_yearly': .55,            # Temp. std. dev. - value from Olonscheck et al. (2021)
                 'sigmaT_daily': 2.,              # Temp. std. dev. - value to be confirmed
                 'corrT': .8,                     # Correlation coeff. of AR(1) process for daily temp. (val. TBC)
                 'Dt_max_da': 30,                 # for Tutorial 2: HW defined over a month max
                 'month': 7,                      # Calendar month (July = 7) when heatwave occurrence explored
                 'lat_deg': grid.par['lat_deg']}
src.par['Li'] = {'object': 'supercell'}
src.par['LS'] = {'object': 'terrain'}
src.par['PI'] = {'object': 'crops',
                 'Si_yieldloss': [50,65],         # event size def. as mean crop loss %tage in entire region
                 'sigmaT_yearly': .55,            # Temp. std. dev. - value from Olonscheck et al. (2021)
                 'month': 7,                      # Calendar month (July = 7) when pest occurrence explored
                 'Tmin_compute': 30.,             # Minimum temperature (°C) to compute PI emergence
                 'lat_deg': grid.par['lat_deg'],
                 'landuse': urbLandLayer.S.copy()}
src.par['RS'] = {'object': 'atmosphere',          # as trigger of landslides
                 'duration': 24}                  # (hr) to calc. soil wetness that triggers LS & FF discharge
                                                  # WARNING: constant for now, to be improved

src.par['SS'] = {'object': 'coastline'}
SS_src_xi, SS_src_yi = topoLayer.coastline_coord
src.SS_char = {'x': SS_src_xi, 'y': SS_src_yi}

src.par['TC'] = {'object': 'stormtrack', 'N': 5,  # pseudo-random track sources moving from West to East
                 'npt': 10,      # number of points along track, which crosses the grid from West to East
                 'max_dev': 3,   # random uniform deviation along the y-axis at each track point
                 'bin_km': 1.}   # track spatial resolution

src.par['To'] = {'object': 'vortexline', 'N': 9,  # random uniform vortex-line initiation points
                 'seed_xmax': 30.,                # initiates within [xmin+xbuffer, seed_xmax], i.e. warmer area
                 'theta_var': 45.,                # maximum angle deviation (°) from West-East direction
                 # beta distributions for stoch. line lengths function of EF size (3 defined: EF-3, EF-4, EF-5)
                 'L_alpha_beta_Lmax_EF3': [.744, 2.87, 100.],
                 'L_alpha_beta_Lmax_EF4': [1.077, 2.36, 100.],
                 'L_alpha_beta_Lmax_EF5': [1.222, 1.767, 100.],
                 'bin_km': 1.}   # line spatial resolution

src.par['WF'] = {'object': 'forest'}
src.par['WS'] = {'object': 'atmosphere'}          # area source instead of track source due to lack of simple model
                                                  # constant vmax for all (x,y) reasonable because grid small

## TECHNOLOGICAL ##
CI_x, CI_y = energyLayer.CI_refinery.centroid
src.par['Ex'] = {'object': 'refinery', 'N': 1, 'x': CI_x, 'y': CI_y}  # harbor refinery as source of explosions
# blackout to add...

## SOCIO-ECONOMIC ##
# to add...

GenMR_perils.plot_src(src, hillshading_z = topoLayer.z, file_ext = 'jpg')

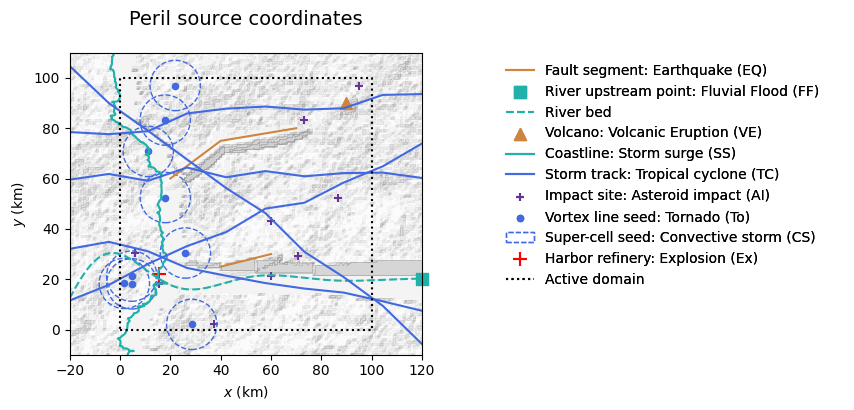
NOTE: Hazard intensity footprints are modeled based on the sources shown in the map above. For stochastic sources (AI, TC, To), rerunning the previous cell will produce different configurations unless rdm_seed is fixed. For To, the full stochastic source (line) can only be parameterised in EventSetGenerator() since its length depends on the event size distribution.

1.2. Event table generation

The stochastic event set (or event table) consists of a list of events per peril, with identifier evID, size S, and rate \(\lambda\) (lbd). Two types of perils are considered: primary perils for which the rate of occurrence must be assessed and secondary perils which will be assumed in this tutorial to occur in pair with their triggers (with rate NaN - for conditional probabilities, see the future Tutorial 3):

• Primary perils: AI, EQ, RS, TC, To, VE, WF, WS.

• Special perils: CS (primary peril depending on characteristics of To secondary peril), Dr (rate calculated independently from calc_lbd_Dr()), HW and PI (rate derived from intensity footprint generation)

• Secondary perils: Li triggered by CS, LS and FF triggered by RS, SS triggered by TC, Ex triggered by damage.

Event size distributions are parameterised in the dictionary sizeDistr with:

• Event size incrementation according Smin, Smax and Sbin with binning in linear or log scale.

• Event size distribution modelled by one of 3 functions: power-law (powerlaw, Mignan, 2024:eq. 2.38), exponential law (exponential, Mignan, 2024:eq. 2.39), or Generalised Pareto Distribution (GPD, Mignan, 2024:eq. 2.50).

• Rates of the digital template are for most perils simply calibrated by taking the ratio of the region area to the area used to obtain event productivity parameters in the Mignan (2024) textbook (e.g., global or continental United States, CONUS). This is a simplification assuming a homogeneous spatial distribution of events but is used as a straightforward way to define rates for the present virtual region. Contradictions may also arise, such as between tropical cyclones (TC) and windstorms (WS), which are not expected to occur within the same latitude range. However, the purpose of this tutorial is to define and illustrate all possible perils. The mutual exclusivity of TC and WS in the same region will be addressed in Tutorial 3. If you wish to avoid this issue in the current tutorial, simply remove either TC or WS from sizedistr['primary'] - possible improvement: include latitude dependence of peril rate).

All calculations take place in the EventSetGenerator() class.

NOTE 1: The maximum possible event size, Smax, is defined by the user for all perils except earthquakes. For earthquakes, the maximum magnitude is constrained by the maximum fault length (src.EQ_char['srcMmax']) according to an empirical relationship (Mignan, 2024:fig. 2.6b).

NOTE 2: A floating rupture approach is used to generate earthquake ruptures on existing fault segments. See Appendix B to visualise the stochastic ruptures created by running the next cell, and refer to the Reference Manual for details on the method.

NOTE 3: The number of stochastic events is set equal to the number of sources when the sources themselves are stochastic (i.e., AI, TC). This number is kep very low for illustration purposes.

NOTE 4: The rate of heatwaves (HW) and of pest infestations (PI) is computed jointly with the generation of their intensity footprints, as their occurrence is governed by extremes in a stochastic spatiotemporal temperature field constrained by the atmospheric environmental layer.

EQ_Mmax = np.max(src.EQ_char['srcMmax'])

sizeDistr = {
    # WARNING: all src.par['perils'] modelled, do not remove perils below if listed in src.par['perils']
    'primary': ['AI','EQ','RS','TC','To','VE','WF','WS'],
    'special': ['CS','Dr','HW','PI'],
    'secondary': ['FF','Li','LS','SS', 'Ex'],
    # primary perils
    'AI':{
        'Nstoch': src.par['AI']['N'], 'Sunit': 'Bolide energy $E$ (kton)',
        'Smin': 10, 'Smax': 1e3, 'Sbin': 1, 'Sscale': 'log',
        'distr': 'powerlaw', 'region': 'global', 'a0': .5677, 'b': .9,      # see Mignan (2024:sect.2.3.1)
        'calibration_source': '',
        'reference': 'to_add'
    },
    'EQ':{
        'Nstoch': 20, 'Sunit': 'Magnitude',
        'Smin': 6, 'Smax': EQ_Mmax, 'Sbin': .1, 'Sscale': 'linear',
        'distr': 'exponential', 'a': 5, 'b': 1.,         # i.e., one M = a-value EQ per year (given b-value = 1)
        'calibration_source': 'user-defined',
        'reference': 'none'
    },
    'RS':{
        'Nstoch': 3, 'Sunit': 'Water column (mm/hr)',
        'Smin': 75, 'Smax': 125, 'Sbin': 25, 'Sscale': 'linear',
        'distr': 'GPD', 'region': 'CONUS', 'mu': 50., 'xi': -.051, 'sigma': 11.8, 'Lbdmin0': 522., 
            # see Mignan (2024:sect.2.3.2)
        'calibration_source': '',
        'reference': 'to_add'
    },
    'TC':{
        'Nstoch': src.par['TC']['N'], 'Sunit': 'Max. wind speed (m/s)',
        'Smin': 40, 'Smax': 65, 'Sbin': 10, 'Sscale': 'linear',
        'distr': 'GPD', 'region': 'global', 'mu': 33., 'xi': -.280, 'sigma': 17.8,'Lbdmin0': 43.9,
#        , 'Lbdmin': .1      # overwrites Lbdmin derived from Lbdmin0 to directly choose rate(>=Smin) = Lbdmin
        'calibration_source': 'IBTrACS',
        'reference': 'to_add'
    },
    'To':{
        'Nstoch': src.par['To']['N'], 'Sunit': 'Enhanced Fujita scale',
        'Smin': 3, 'Smax': 5, 'Sbin': 1, # WARNING: hardcoded, do not change, depends on 'L_alpha_beta_Lmax_EF*'
        'Sscale': 'linear',
        'distr': 'exponential', 'region': 'CONUS', 'a0': 3.6, 'b': .9,
        'calibration_source': 'NOAA 1950-2021 tornadoes (public)',
        'reference': 'to_add'
    },
    'VE':{
        'Nstoch': 3, 'Sunit': 'Ash volume (km$^3$)',
        'Smin': 1, 'Smax': 10, 'Sbin': .5, 'Sscale': 'log',
        'distr': 'powerlaw', 'region': 'global', 'a0': -1.155, 'b': .66,      # see Sect. 2.3.1
        'calibration_source': '',
        'reference': 'to_add'
    },
    'WF':{
        'Nstoch': 10, 'Sunit': 'Burnt area (ha)',
        'Smin': 1e4, 'Smax': 1e5, 'Sbin': .5, 'Sscale': 'log',
        'distr': 'powerlaw', 'region': 'global', 'a0': 8.553, 'b': 1.23,      # see Sect. 2.3.1
        'calibration_source': '',
        'reference': 'to_add'
    },
    'WS':{
        'Nstoch': 2, 'Sunit': 'Max. wind speed (m/s)',
        'Smin': 45, 'Smax': 50, 'Sbin': 5, 'Sscale': 'linear',
        'distr': 'GPD', 'region': 'local', 'mu': 17., 'xi': -.112, 'sigma': 4.43, 'Lbdmin': 163.25,
        # GPD params. for Brest (France) location for illustration purposes (consider making it func. of lat.)
        'calibration_source': 'Copernicus 1986-2011 Synthetic windstorm events for Europe',
        'reference': '10.24381/cds.ce973f02'
    },
    # special perils
    'CS':{                # CS triggers To but To param better constrained, backpropagating to CS
        'Nstoch': src.par['To']['N']
    },
    'Dr':{                # Dr event rates to be calculated in calc_lbd_Dr() - see next code cell
        'Nstoch': len(src.par['Dr']['Si_mo'])        
    },
    'HW':{                # HW event rates to be calculated alongside footprint generation
        'Nstoch': len(src.par['HW']['Si_da'])
    },
    'PI':{                # PI event rates to be calculated alongside footprint generation
        'Nstoch': len(src.par['PI']['Si_yieldloss'])
    },
    # secondary perils - here ad-hoc Pr(peril|trigger) = 1, see tutorial 3 for probabilistic case
    'FF':{'trigger': 'RS'},
    'Li':{'trigger': 'CS'},
    'LS':{'trigger': 'RS'},
    'SS':{'trigger': 'TC'},
    'Ex':{'trigger': 'dg',     # 'dg' label indicates event triggered by damage caused by any peril (tutorial 3)
          'S': 1., 'Sunit': 'Explosive yield (kton)'
    }
}

eventSet = GenMR_perils.EventSetGenerator(src, sizeDistr, GenMR_utils)
evtable, evchar = eventSet.generate()

#evtable
with pd.option_context('display.max_rows', None,
                       'display.max_columns', None):
    display(evtable)

	ID	srcID	evID	S	lbd
0	AI	impact1	AI1	10.000000	2.657777e-06
1	AI	impact2	AI2	10.000000	2.657777e-06
2	AI	impact3	AI3	10.000000	2.657777e-06
3	AI	impact4	AI4	100.000000	2.509457e-07
4	AI	impact5	AI5	100.000000	2.509457e-07
5	AI	impact6	AI6	100.000000	2.509457e-07
6	AI	impact7	AI7	100.000000	2.509457e-07
7	AI	impact8	AI8	1000.000000	4.212292e-08
8	AI	impact9	AI9	1000.000000	4.212292e-08
9	AI	impact10	AI10	1000.000000	4.212292e-08
10	Dr	soil	Dr1	3.000000	NaN
11	Dr	soil	Dr2	6.000000	NaN
12	Dr	soil	Dr3	9.000000	NaN
13	EQ	fault1	EQ1	6.000000	6.855726e-03
14	EQ	fault2	EQ2	6.000000	6.855726e-03
15	EQ	fault1	EQ3	6.000000	6.855726e-03
16	EQ	fault1	EQ4	6.100000	5.445696e-03
17	EQ	fault1	EQ5	6.100000	5.445696e-03
18	EQ	fault1	EQ6	6.100000	5.445696e-03
19	EQ	fault1	EQ7	6.200000	6.488506e-03
20	EQ	fault1	EQ8	6.200000	6.488506e-03
21	EQ	fault1	EQ9	6.300000	3.436002e-03
22	EQ	fault1	EQ10	6.300000	3.436002e-03
23	EQ	fault1	EQ11	6.300000	3.436002e-03
24	EQ	fault1	EQ12	6.400000	4.093970e-03
25	EQ	fault1	EQ13	6.400000	4.093970e-03
26	EQ	fault2	EQ14	6.500000	3.251956e-03
27	EQ	fault1	EQ15	6.500000	3.251956e-03
28	EQ	fault1	EQ16	6.600000	5.166241e-03
29	EQ	fault1	EQ17	6.700000	4.103691e-03
30	EQ	fault1	EQ18	6.800000	3.259678e-03
31	EQ	fault1	EQ19	6.900000	2.589254e-03
32	EQ	fault1	EQ20	7.000000	2.056718e-03
33	HW	atmosphere	HW1	7.000000	NaN
34	HW	atmosphere	HW2	14.000000	NaN
35	HW	atmosphere	HW3	30.000000	NaN
36	PI	crops	PI1	50.000000	NaN
37	PI	crops	PI2	65.000000	NaN
38	RS	atmosphere	RS1	75.000000	1.000793e-03
39	RS	atmosphere	RS2	100.000000	8.172054e-05
40	RS	atmosphere	RS3	125.000000	4.562873e-06
41	TC	stormtrack1	TC1	40.000000	2.841439e-04
42	TC	stormtrack2	TC2	50.000000	1.637893e-04
43	TC	stormtrack3	TC3	60.000000	4.064719e-05
44	TC	stormtrack4	TC4	60.000000	4.064719e-05
45	TC	stormtrack5	TC5	70.000000	3.110718e-05
46	To	vortexline1	To1	3.000000	4.537519e-05
47	To	vortexline2	To2	3.000000	4.537519e-05
48	To	vortexline3	To3	3.000000	4.537519e-05
49	To	vortexline4	To4	4.000000	5.712399e-06
50	To	vortexline5	To5	4.000000	5.712399e-06
51	To	vortexline6	To6	4.000000	5.712399e-06
52	To	vortexline7	To7	5.000000	7.191484e-07
53	To	vortexline8	To8	5.000000	7.191484e-07
54	To	vortexline9	To9	5.000000	7.191484e-07
55	VE	volcano1	VE1	1.000000	7.303024e-07
56	VE	volcano1	VE2	3.162278	3.415881e-07
57	VE	volcano1	VE3	10.000000	1.597728e-07
58	WF	forest	WF1	10000.000000	1.062953e-02
59	WF	forest	WF2	10000.000000	1.062953e-02
60	WF	forest	WF3	10000.000000	1.062953e-02
61	WF	forest	WF4	10000.000000	1.062953e-02
62	WF	forest	WF5	10000.000000	1.062953e-02
63	WF	forest	WF6	10000.000000	1.062953e-02
64	WF	forest	WF7	31622.776602	5.158744e-03
65	WF	forest	WF8	31622.776602	5.158744e-03
66	WF	forest	WF9	31622.776602	5.158744e-03
67	WF	forest	WF10	100000.000000	3.755478e-03
68	WS	atmosphere	WS1	45.000000	2.741867e-03
69	WS	atmosphere	WS2	50.000000	1.746819e-05
70	CS	supercell	CS_toTo1	13.811900	NaN
71	CS	supercell	CS_toTo2	13.811900	NaN
72	CS	supercell	CS_toTo3	13.811900	NaN
73	CS	supercell	CS_toTo4	13.811900	NaN
74	CS	supercell	CS_toTo5	13.811900	NaN
75	CS	supercell	CS_toTo6	13.811900	NaN
76	CS	supercell	CS_toTo7	13.811900	NaN
77	CS	supercell	CS_toTo8	13.811900	NaN
78	CS	supercell	CS_toTo9	13.811900	NaN
79	Ex	refinery	Ex_fromCIf	1.000000	NaN
80	FF	river1	FF_fromRS1	NaN	NaN
81	FF	river1	FF_fromRS2	NaN	NaN
82	FF	river1	FF_fromRS3	NaN	NaN
83	Li	supercell	Li_fromCS1	NaN	NaN
84	Li	supercell	Li_fromCS2	NaN	NaN
85	Li	supercell	Li_fromCS3	NaN	NaN
86	Li	supercell	Li_fromCS4	NaN	NaN
87	Li	supercell	Li_fromCS5	NaN	NaN
88	Li	supercell	Li_fromCS6	NaN	NaN
89	Li	supercell	Li_fromCS7	NaN	NaN
90	Li	supercell	Li_fromCS8	NaN	NaN
91	Li	supercell	Li_fromCS9	NaN	NaN
92	LS	terrain	LS_fromRS1	NaN	NaN
93	LS	terrain	LS_fromRS2	NaN	NaN
94	LS	terrain	LS_fromRS3	NaN	NaN
95	SS	coastline	SS_fromTC1	NaN	NaN
96	SS	coastline	SS_fromTC2	NaN	NaN
97	SS	coastline	SS_fromTC3	NaN	NaN
98	SS	coastline	SS_fromTC4	NaN	NaN
99	SS	coastline	SS_fromTC5	NaN	NaN

Running the EventSetGenerator is effectively instantaneous. In contrast, computing drought (Dr) rates requires several minutes and is therefore executed as a separate step (see below). The calculation is based on a water-balance model in which soil water content evolves from an initial state (defined by the soil layer’s 'moisture_regime') and is subsequently modulated by evapotranspiration (see calc_PET()) and precipitation (see gen_precipitation()) over the twelve months of a calendar year. Conditions conducive to drought development arise during anticyclonic years, when accompanied by anomalously high summer temperatures.

Note: The correlation between Dr, HW, PI, and the anticorrelation with RS, will be examined in Tutorial 3.

## optional cell ##

rates_Dr = GenMR_perils.calc_lbd_Dr(src.par['Dr'], atmoLayer.par, soilLayer.par)
evtable.loc[evtable['evID'].str[:2] == 'Dr', 'lbd'] = rates_Dr

Simulating droughts: 100%|██████████| 1000000/1000000 [07:59<00:00, 2087.64it/s]

The evchar dataframe contains the coordinates of the events defined in evtable. The following code cell allows the user to plot stochastic events via their evID:

#print('total list of modelled events, by evID:', evtable['evID'].unique())

## SELECT EVENTS ##
evID_list = ['EQ1','TC1','CS_toTo1', 'To1','Li_fromCS1']
#evID_list = evtable['evID'].values
###################

n_evID = len(evID_list)

max_cols = 5
ncols = min(n_evID, max_cols)
nrows = int(np.ceil(n_evID / ncols))

evID_coords = evchar[evchar['evID'].isin(evID_list)].reset_index(drop = True)

plt.rcParams['font.size'] = '16'
fig, ax = plt.subplots(nrows, ncols, figsize=(4 * ncols, 4 * nrows), squeeze=False)
ax = ax.flatten()
for i in range(n_evID):
    peril_evID = evID_list[i][:2]
    if peril_evID in ['AI', 'VE', 'Li']:
        plot_type = 'scatter'
    elif  peril_evID in ['EQ', 'TC', 'To', 'CS', 'SS']:
        plot_type = 'plot'
    coords2plt = evID_coords[evID_coords['evID'] == evID_list[i]]
    ax[i].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
    if plot_type == 'plot':
        ax[i].plot(coords2plt['x'], coords2plt['y'], color = 'darkred', linewidth = 2)
    elif plot_type == 'scatter':
        ax[i].scatter(coords2plt['x'], coords2plt['y'], color = 'darkred', linewidth = 2)
    ax[i].set_xlim(grid.xmin, grid.xmax)
    ax[i].set_ylim(grid.ymin, grid.ymax)
    ax[i].set_xlabel('$x$ (km)')
    ax[i].set_ylabel('$y$ (km)')
    ax[i].set_title(evID_list[i], pad = 10)
    ax[i].set_aspect(1)

for j in range(n_evID, len(ax)):
    ax[j].axis('off')
    
plt.tight_layout();

1.3. Intensity footprint catalogue generation

Once the event table has been generated, the next step is to produce one mean hazard-intensity footprint per event. Aleatory uncertainty is not implemented for simplicity, and because it does not affect the objectives of this project, namely, modelling compound events in a virtual environment (see the third and final tutorial).

1.3.1. From analytical expressions & threshold models

1.3.1.1. Analytical expressions

Analytical expressions are available to calculate intensity \(I(x,y) = f_I(S,r)\) for the AI/Ex, EQ, VE and TC perils (Mignan, 2024:sec. 2.4.1). The size \(S\) is provided in evtable, while the distance-to-source \(r\) is obtained by matching each event to its corresponding source coordinates via evchar. Because generating TC footprints requires a multi-step procedure, additional details are provided in Appendix C.

The models are implemented as calc_I_*(S,r) functions in the Python file, using the equations from Mignan (2024:sec. 2.4.1):

ID	Event size \(S\)	Intensity \(I\)	Equation
AI, Ex	Explosive mass \(m_{TNT}\) (kt)	Blast overpressure \(P\) (kPa)	Eq. 2.56
EQ	Magnitude \(M\)	Peak ground acceleration PGA (m/s\(^2\))	Eq. 2.54
Li	-	Lightning strike count (/convective storm)	to add
TC	Maximum wind speed \(v_{max}\) (m/s)	Wind speed \(v\) (m/s)	Eq. 2.24
To	Enhanced Fujita (EF) scale to max. wind speed (m/s)	Max. wind speed \(v_{max}\) (m/s)	Eq. 2.59
VE	Erupted volume \(V\) (km\(^3\))	Ash load \(P\) (kPa), converted from thickness (m)	Eq. 2.61

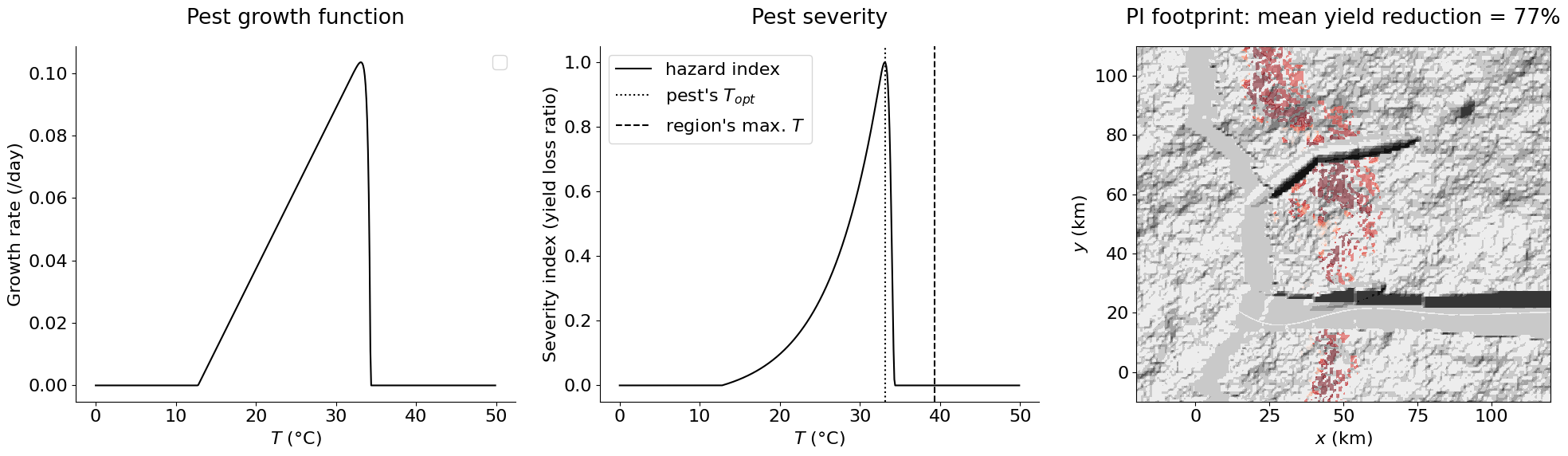
Note that the analytical expression of pest infestation (PI) intensity is of the form \(I(x,y) = f_I(T(x,y))\) with \(T(x,y)\) the near-surface air temperature in the digital template (eq. to add). The footprint is only defined for the land-use state \(S\) = 5 or 6 (crops: wheat or maize - see the model_PI_analytical() function).

1.3.1.2. Threshold models

• Heatwave (HW): Based on an event being declared when the near-surface air temperature equals or exceeds T_th for at least Dt_da consecutive days. Temperature extremes in the digital template arise from the combination of large-scale advective temperature anomalies and temporally correlated daily temperature variability (see the model_HW_threshold() function). It should be noted that, for a given event size S, the largest spatial footprint (i.e., the most extreme realization) is selected from a larger stochastic event set (see all candidate footprints in figs/HW_stochset_tmp/).

• Storm surge (SS): Based on the Bathtub model (Mignan, 2024:sec. 2.4.2). The algorithm is intentionally simple and tailored to the virtual environment used here, where the background topography exhibits a predominantly west-east gradient (see the model_SS_Bathtub() function). As a secondary peril triggered by TC events, the SS size along the coastline is derived from a relationship of the form \(h_{max} \propto v_{max}^2\) (Mignan, 2024:fig. 2.7), where \(v_{max}\) is the wind speed along the coastline obtained from the TC footprint.

Note that rainstorm (RS) and windstorm (WS) footprints are considered spatially homogeneous (prior to the application of any site-specific conditions, which will be addressed subsequently) due to the relatively small size of the active domain of the digital template. Accordingly, their source classes are defined as area sources, and their intensity classes are defined using thresholds, with the threshold value corresponding to the event size S by construction.

The catalogue of hazard footprints is generated via the HazardFootprintGenerator(() class and is visualised with plot_hazFootprints().

src.par['TC']['vforward_m/s'] = 10.         # forward storm speed (m/s)
src.par['TC']['pn_mbar'] = 1005.            # ambient pressure (mbar) - NB: consider using atm. layer p0
src.par['TC']['B_Holland'] = 2              # Holland's parameter (see Fig. 2.10 of textbook)
src.par['TC']['lat_deg'] = grid.lat_deg     # average latitude of digital template (see Tutorial 1)

src.par['To']['Rmax_m'] = 300.              # user-defined, independent of EF scale since no model available
                                            # high value used for illustration

# virtual region bathymetry characteristics for SS height given storm wind speed
src.par['SS']['bathy'] = 'New York harbor'  # 'generic' (Saffir-Simpson, Mignan, 2024:eq. 2.16) 
                                            # 'New York harbor' (eq. in Mignan, 2024:fig. 2.7)

## TO ADD: site-specific conditions ##
# surface friction -> reduce windspeed (TC, WS)
# soil amplification -> increase ground shaking (EQ)
# urban heat island -> increase temperature (HW)
# other?

hazFootprints = GenMR_perils.HazardFootprintGenerator(evtable, evchar, src, topoLayer.z, atmoLayer)
catalog_hazFootprints = hazFootprints.generate()

generating footprints for: AI... Dr... EQ... HW... (loading from cache)
PI... (loading from cache)
RS... TC... To... VE... WF... WS... CS... Ex... FF... Li... LS... SS... catalogue completed

# max intensity Imax in color range (see units in previous table)
# to compare similar levels of expected damage, choose a value per peril for a constant MDR in the vulnerability
# curves (see curves generated by plot_vulnFunctions())
Imax_Ex_totaldestruction = 4 * 6.89476  # kPa (here 4 psi as threshold of total destruction)

plot_Imax = {'AI': Imax_Ex_totaldestruction, 'EQ': 6, 'Ex': Imax_Ex_totaldestruction, \
             'HW': src.par['HW']['T_th'] + 5, 'LS': 2., 'PI': 1,\
             'SS': 2., 'TC': 70., 'To': 70., 'VE': .5, 'WS': 70.}
f = .1
plot_Imin = {'AI': f*plot_Imax['AI'], 'EQ': f*plot_Imax['EQ'], 'Ex': f*plot_Imax['Ex'], \
             'HW': src.par['HW']['T_th'], 'LS': f*plot_Imax['LS'], 'PI': 0, 'SS': f*plot_Imax['SS'], \
             'TC': 30., 'To': 30., 'VE': f*plot_Imax['VE'], 'WS': 30.}

# nstoch (default = 5) defines the number of events per peril to be displayed by row
# if the number of events > nstoch, footprints are randomly sampled from all possibilities
GenMR_perils.plot_hazFootprints(catalog_hazFootprints, grid, topoLayer.z, plot_Imin, plot_Imax)  #, nstoch = 5)

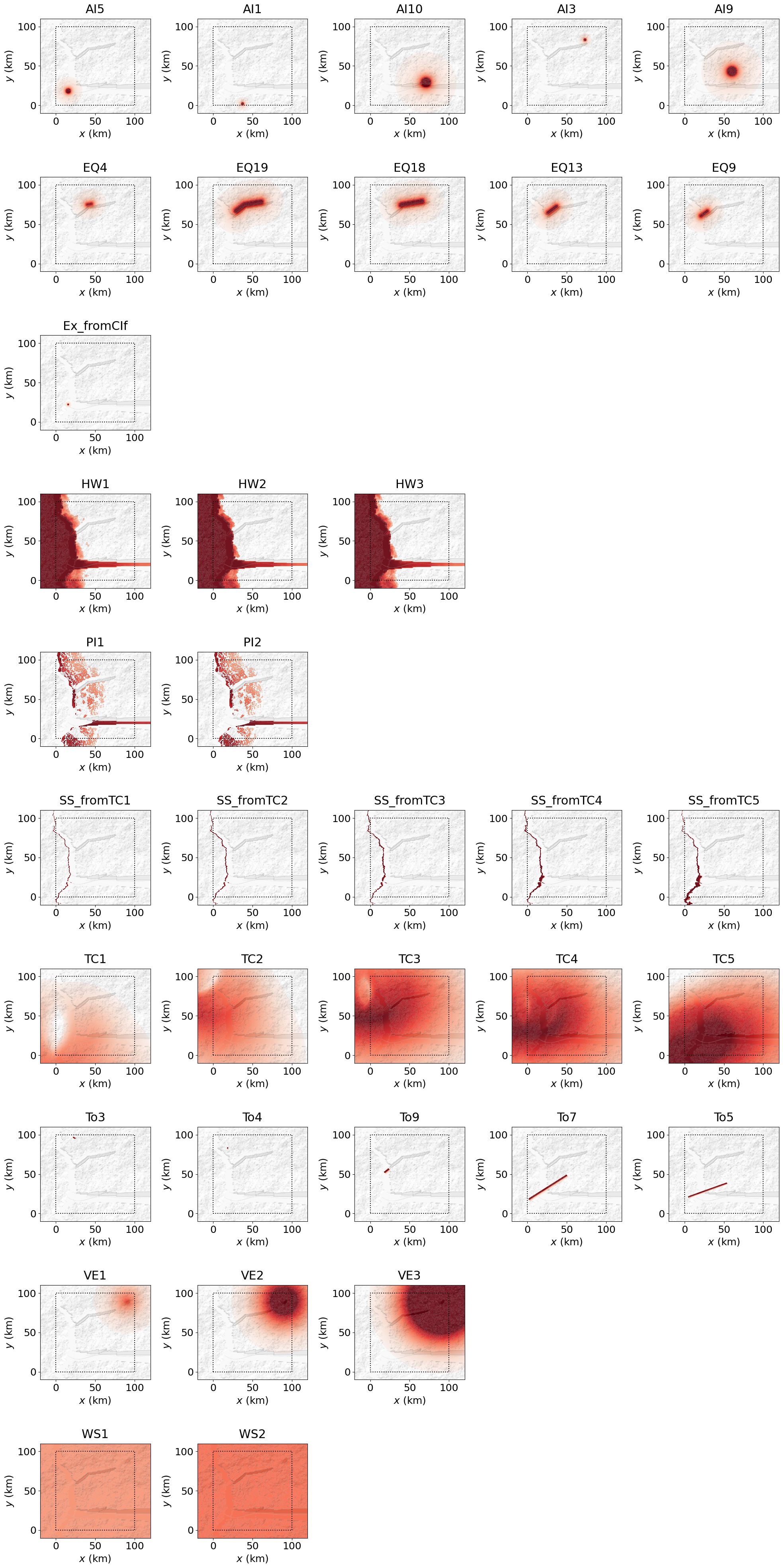
Note: Observe the TC footprint boundary effect (cyclonic eye), which is due to the track artificially starting at grid.xmin.

It was previously indicated that the HW and PI event rates are computed jointly with the generation of their intensity footprints. It is possible to retrieve these rates from:

rates_HW = hazFootprints.rate_HW
rates_PI = hazFootprints.rate_PI

# update event table
evtable.loc[evtable['evID'].str[:2] == 'HW', 'lbd'] = rates_HW
evtable.loc[evtable['evID'].str[:2] == 'PI', 'lbd'] = rates_PI

with pd.option_context('display.max_rows', None):
    display(evtable)

	ID	srcID	evID	S	lbd
0	AI	impact1	AI1	10.000000	2.657777e-06
1	AI	impact2	AI2	10.000000	2.657777e-06
2	AI	impact3	AI3	10.000000	2.657777e-06
3	AI	impact4	AI4	100.000000	2.509457e-07
4	AI	impact5	AI5	100.000000	2.509457e-07
5	AI	impact6	AI6	100.000000	2.509457e-07
6	AI	impact7	AI7	100.000000	2.509457e-07
7	AI	impact8	AI8	1000.000000	4.212292e-08
8	AI	impact9	AI9	1000.000000	4.212292e-08
9	AI	impact10	AI10	1000.000000	4.212292e-08
10	Dr	soil	Dr1	3.000000	NaN
11	Dr	soil	Dr2	6.000000	NaN
12	Dr	soil	Dr3	9.000000	NaN
13	EQ	fault1	EQ1	6.000000	6.855726e-03
14	EQ	fault2	EQ2	6.000000	6.855726e-03
15	EQ	fault1	EQ3	6.000000	6.855726e-03
16	EQ	fault1	EQ4	6.100000	5.445696e-03
17	EQ	fault1	EQ5	6.100000	5.445696e-03
18	EQ	fault1	EQ6	6.100000	5.445696e-03
19	EQ	fault1	EQ7	6.200000	6.488506e-03
20	EQ	fault1	EQ8	6.200000	6.488506e-03
21	EQ	fault1	EQ9	6.300000	3.436002e-03
22	EQ	fault1	EQ10	6.300000	3.436002e-03
23	EQ	fault1	EQ11	6.300000	3.436002e-03
24	EQ	fault1	EQ12	6.400000	4.093970e-03
25	EQ	fault1	EQ13	6.400000	4.093970e-03
26	EQ	fault2	EQ14	6.500000	3.251956e-03
27	EQ	fault1	EQ15	6.500000	3.251956e-03
28	EQ	fault1	EQ16	6.600000	5.166241e-03
29	EQ	fault1	EQ17	6.700000	4.103691e-03
30	EQ	fault1	EQ18	6.800000	3.259678e-03
31	EQ	fault1	EQ19	6.900000	2.589254e-03
32	EQ	fault1	EQ20	7.000000	2.056718e-03
33	HW	atmosphere	HW1	7.000000	7.400000e-04
34	HW	atmosphere	HW2	14.000000	1.700000e-04
35	HW	atmosphere	HW3	30.000000	1.000000e-05
36	PI	crops	PI1	50.000000	3.950000e-03
37	PI	crops	PI2	65.000000	0.000000e+00
38	RS	atmosphere	RS1	75.000000	1.000793e-03
39	RS	atmosphere	RS2	100.000000	8.172054e-05
40	RS	atmosphere	RS3	125.000000	4.562873e-06
41	TC	stormtrack1	TC1	40.000000	2.841439e-04
42	TC	stormtrack2	TC2	50.000000	1.637893e-04
43	TC	stormtrack3	TC3	60.000000	4.064719e-05
44	TC	stormtrack4	TC4	60.000000	4.064719e-05
45	TC	stormtrack5	TC5	70.000000	3.110718e-05
46	To	vortexline1	To1	3.000000	4.537519e-05
47	To	vortexline2	To2	3.000000	4.537519e-05
48	To	vortexline3	To3	3.000000	4.537519e-05
49	To	vortexline4	To4	4.000000	5.712399e-06
50	To	vortexline5	To5	4.000000	5.712399e-06
51	To	vortexline6	To6	4.000000	5.712399e-06
52	To	vortexline7	To7	5.000000	7.191484e-07
53	To	vortexline8	To8	5.000000	7.191484e-07
54	To	vortexline9	To9	5.000000	7.191484e-07
55	VE	volcano1	VE1	1.000000	7.303024e-07
56	VE	volcano1	VE2	3.162278	3.415881e-07
57	VE	volcano1	VE3	10.000000	1.597728e-07
58	WF	forest	WF1	10000.000000	1.062953e-02
59	WF	forest	WF2	10000.000000	1.062953e-02
60	WF	forest	WF3	10000.000000	1.062953e-02
61	WF	forest	WF4	10000.000000	1.062953e-02
62	WF	forest	WF5	10000.000000	1.062953e-02
63	WF	forest	WF6	10000.000000	1.062953e-02
64	WF	forest	WF7	31622.776602	5.158744e-03
65	WF	forest	WF8	31622.776602	5.158744e-03
66	WF	forest	WF9	31622.776602	5.158744e-03
67	WF	forest	WF10	100000.000000	3.755478e-03
68	WS	atmosphere	WS1	45.000000	2.741867e-03
69	WS	atmosphere	WS2	50.000000	1.746819e-05
70	CS	supercell	CS_toTo1	13.811900	NaN
71	CS	supercell	CS_toTo2	13.811900	NaN
72	CS	supercell	CS_toTo3	13.811900	NaN
73	CS	supercell	CS_toTo4	13.811900	NaN
74	CS	supercell	CS_toTo5	13.811900	NaN
75	CS	supercell	CS_toTo6	13.811900	NaN
76	CS	supercell	CS_toTo7	13.811900	NaN
77	CS	supercell	CS_toTo8	13.811900	NaN
78	CS	supercell	CS_toTo9	13.811900	NaN
79	Ex	refinery	Ex_fromCIf	1.000000	NaN
80	FF	river1	FF_fromRS1	NaN	NaN
81	FF	river1	FF_fromRS2	NaN	NaN
82	FF	river1	FF_fromRS3	NaN	NaN
83	Li	supercell	Li_fromCS1	NaN	NaN
84	Li	supercell	Li_fromCS2	NaN	NaN
85	Li	supercell	Li_fromCS3	NaN	NaN
86	Li	supercell	Li_fromCS4	NaN	NaN
87	Li	supercell	Li_fromCS5	NaN	NaN
88	Li	supercell	Li_fromCS6	NaN	NaN
89	Li	supercell	Li_fromCS7	NaN	NaN
90	Li	supercell	Li_fromCS8	NaN	NaN
91	Li	supercell	Li_fromCS9	NaN	NaN
92	LS	terrain	LS_fromRS1	NaN	NaN
93	LS	terrain	LS_fromRS2	NaN	NaN
94	LS	terrain	LS_fromRS3	NaN	NaN
95	SS	coastline	SS_fromTC1	NaN	NaN
96	SS	coastline	SS_fromTC2	NaN	NaN
97	SS	coastline	SS_fromTC3	NaN	NaN
98	SS	coastline	SS_fromTC4	NaN	NaN
99	SS	coastline	SS_fromTC5	NaN	NaN

1.3.2. From numerical models (cellular automata)

Generation of hazard-intensity footprints via dynamical processes (here, cellular automata - CA) is handled separately because these computations are more expensive. This functionality is implemented in the DynamicHazardFootprintGenerator() class and applied to the LS, FF and WF perils. Details of the corresponding CA models can be found in the Python file within the CellularAutomaton_* classes, where * denotes the peril ID.

The following movie illustrates an example of dynamical process. It is produced by running LS_CA.write_gif() in the next cell and shows the time-evolving landslide propagation generated by the CA. The final hazard-intensity footprint included in the hazard-footprint catalogue is static and defined as \(\max_t I(x,y,t)\).

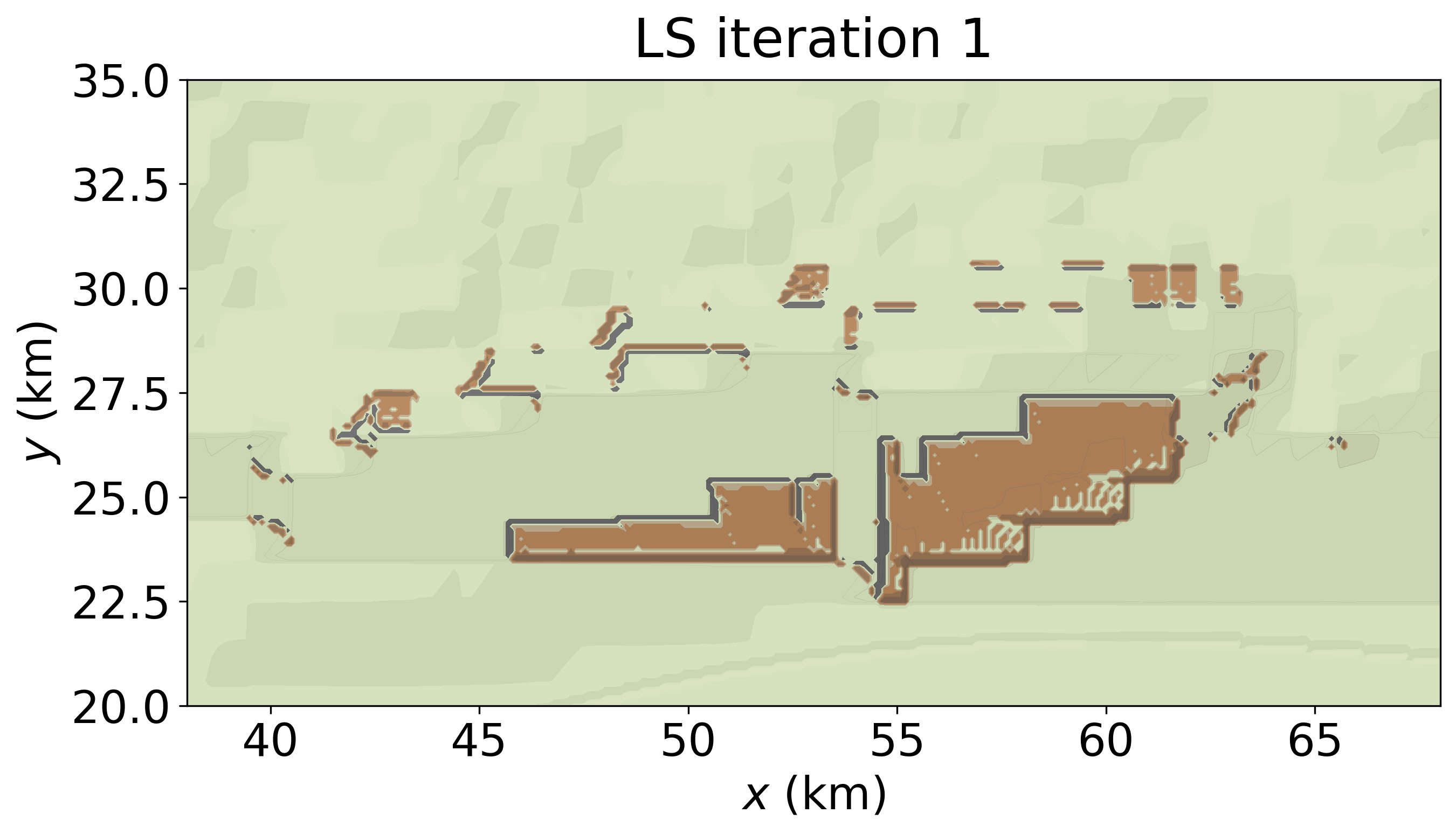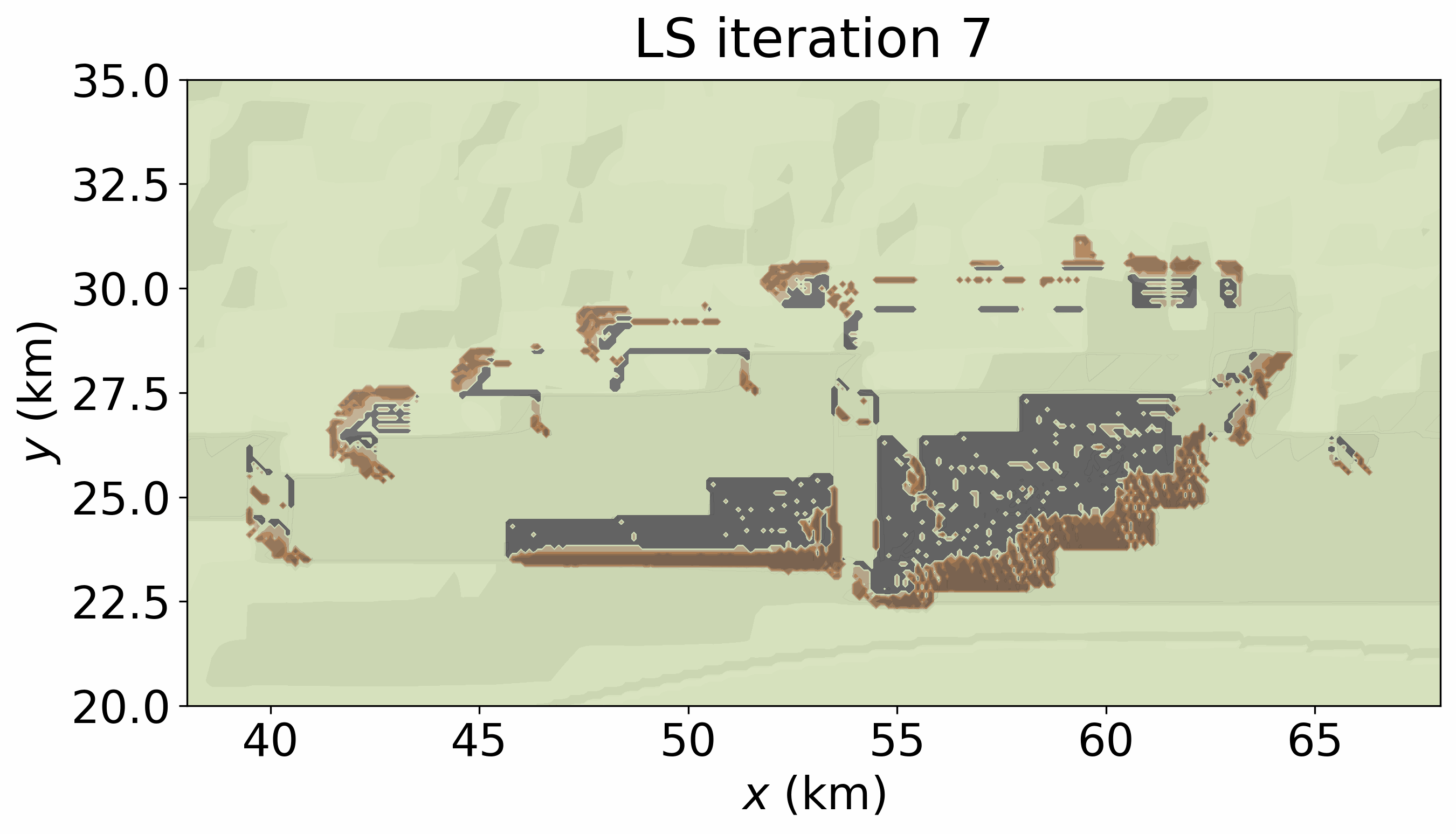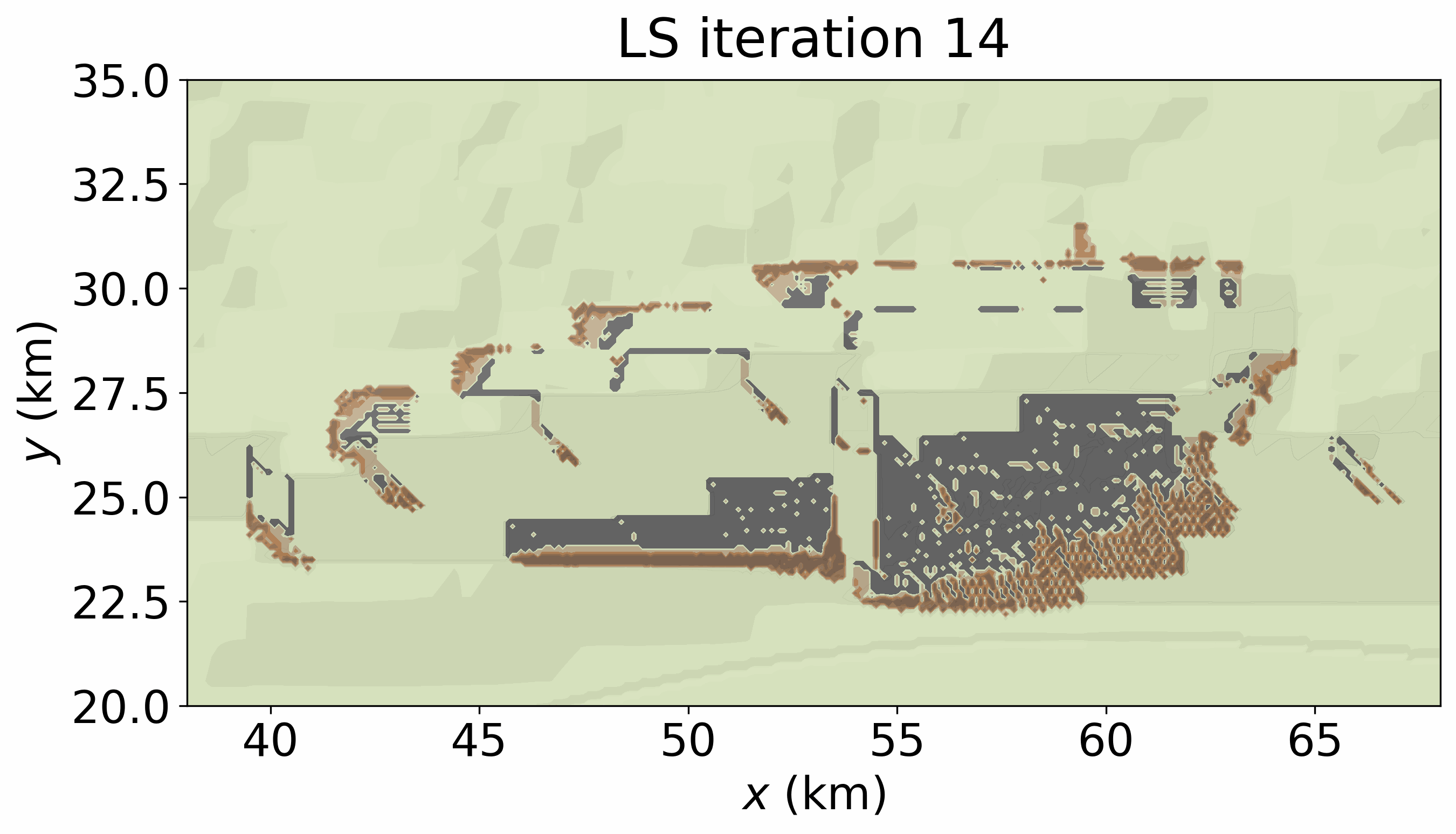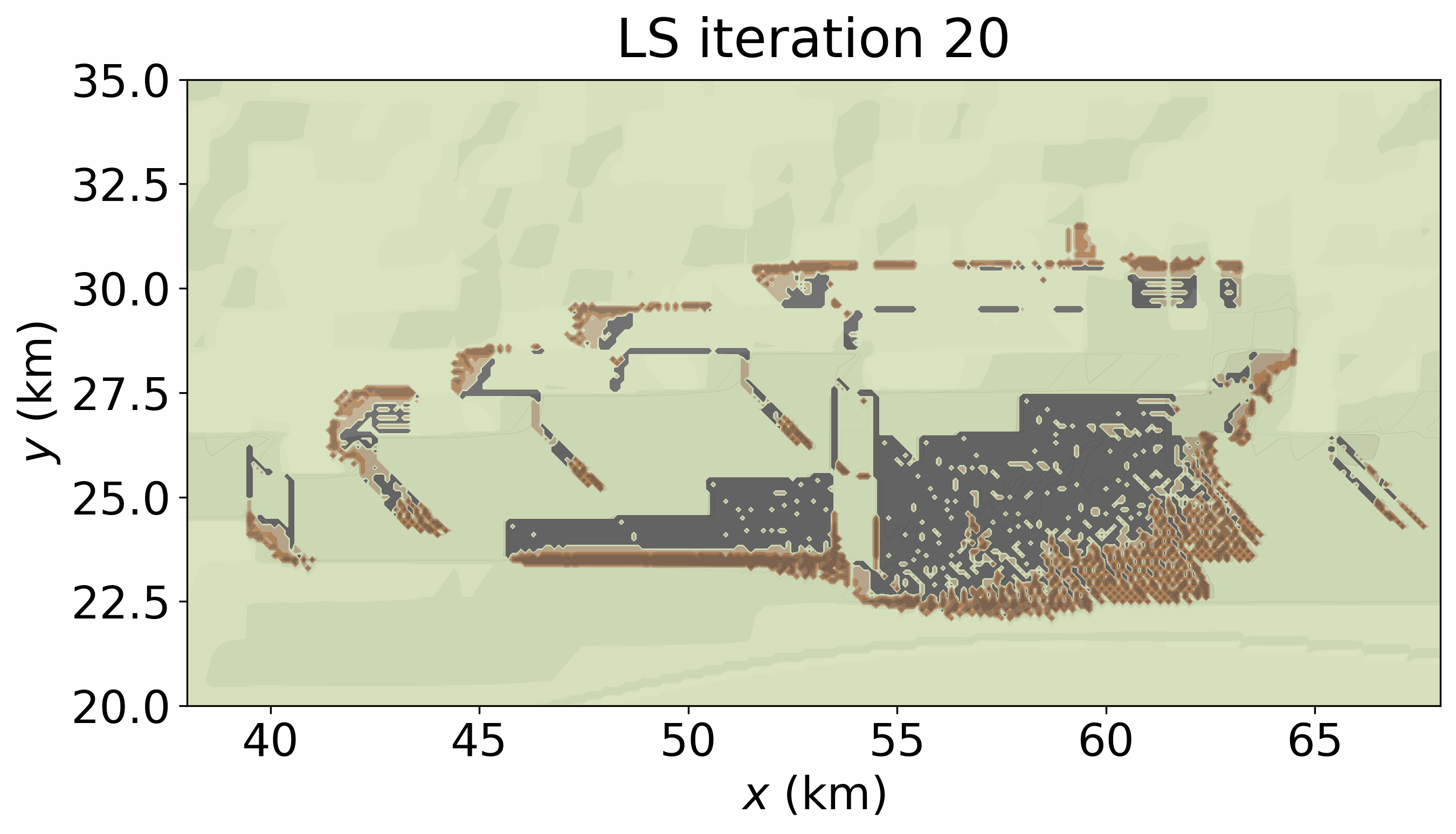
reproduce_LSmovie = False          # True to create 'movs/LS_CA_xrg38_68_yrg20_35.gif'
reproduce_FFmovie = False          # True to create 'movs/FF_CA_xrg0_100_yrg0_40.gif'

if reproduce_LSmovie:
    movie = {'create': True, 'xmin': 38, 'xmax': 68, 'ymin': 20, 'ymax': 35}   # zoom on specific hill

    evID_trigger = 'RS3'                                       # case considered for movie scenario
    S_trigger = evtable['S'][evtable['evID'] == evID_trigger].values
    hw = S_trigger * 1e-3 * src.par['RS']['duration']          # water column (m)
    wetness = hw / soilLayer.h
    wetness[wetness > 1] = 1                                   # max possible saturation
    wetness[soilLayer.h == 0] = 0                              # no soil case

    LS_CA = GenMR_perils.CellularAutomaton_LS(soilLayer, wetness, movie)
    LS_CA.run()
    LS_CA.write_gif()
    print()
    print('LS movie created (go to mov/LS_CA_*).')
else:
    print('No LS movie created.')
    
if reproduce_FFmovie:
    I_RS = evtable[evtable['evID'] == 'RS3']['S'].values[0] * 1e-3 / 3600    # (mm/hr) to (m/s)
    movie = {'create': True, 'xmin': 0, 'xmax': 100, 'ymin': 0, 'ymax': 40, 'tmin': 40} 

    FF_CA = GenMR_perils.CellularAutomaton_FF(I_RS, src, grid, topoLayer.z, movie)
    FF_CA.run()
    FF_CA.write_gif()
    print()
    print('FF movie created (go to mov/FF_CA_*).')
else:
    print('No FF movie created.')

No LS movie created.
23.0 hr / 24.0
FF movie created (go to mov/FF_CA_*).

Footprints are initialised in dynhazFootprints, an instance of the DynamicHazardFootprintGenerator() class. Running dynhazFootprints.generate() computes all dynamical intensity footprints at once. To generate only a specific subset of perils, one must use dynhazFootprints.generate(selected_perils = ['LS', 'FF', ...]). Note that if a peril has already been run, cached footprints will be loaded automatically. To force recomputation, one needs to include the option force_recompute = True in the class command (or delete the folder *_CA_frames).

# additional WF source/landuse parameters
src.par['WF'] = {'ratio_grass': .6,        # ratio of forest cells to turn to grass at initial state
             'p_lightning': .1,            # probability of lightning strike per iteration
             'rate_newtrees': 1000,        # number of new trees to add per iteration
             'nsim': 100000,               # number of iterations
             'Smin_plot': 1000,            # minimum WF footprint size to save in 'figs/WF_CA_frames'
            }

dynhazFootprints = GenMR_perils.DynamicHazardFootprintGenerator(evtable, src, soilLayer, urbLandLayer)
catalog_dynhazFootprints = dynhazFootprints.generate()
#_ = dynhazFootprints.generate(selected_perils = ['LS'], force_recompute = True)
#catalog_dynhazFootprints = dynhazFootprints.generate(selected_perils = ['FF'], force_recompute = True)
catalog_dynhazFootprints.keys()

generating footprints for:
Loading from cache potential footprints

Fetching footprints from potential footprints

Fetching WF footprints from cache: 100%|████████| 10/10 [00:00<00:00, 48.55it/s]

FF_fromRS1 (computing)
0.0 hr / 24.0

FF_fromRS2 (computing)
FF_fromRS3 (computing)
LS_fromRS1 (loaded from cache)
LS_fromRS2 (loaded from cache)
LS_fromRS3 (loaded from cache)
... catalogue completed

dict_keys(['WF1', 'WF2', 'WF3', 'WF4', 'WF5', 'WF6', 'WF7', 'WF8', 'WF9', 'WF10', 'FF_fromRS1', 'FF_fromRS2', 'FF_fromRS3', 'LS_fromRS1', 'LS_fromRS2', 'LS_fromRS3'])

try:
    plot_Imin.update({'LS': 0, 'FF': 0, 'WF': 0})
    plot_Imax.update({'LS': 2, 'FF': 1, 'WF': 1})
except NameError:
    plot_Imin = {'LS': 0, 'FF': 0, 'WF': 0}
    plot_Imax = {'LS': 2, 'FF': 1, 'WF': 1}

catalog_dynhazFootprints = dynhazFootprints.catalog_hazFootprints
GenMR_perils.plot_hazFootprints(catalog_dynhazFootprints, grid, topoLayer.z, plot_Imin, plot_Imax)

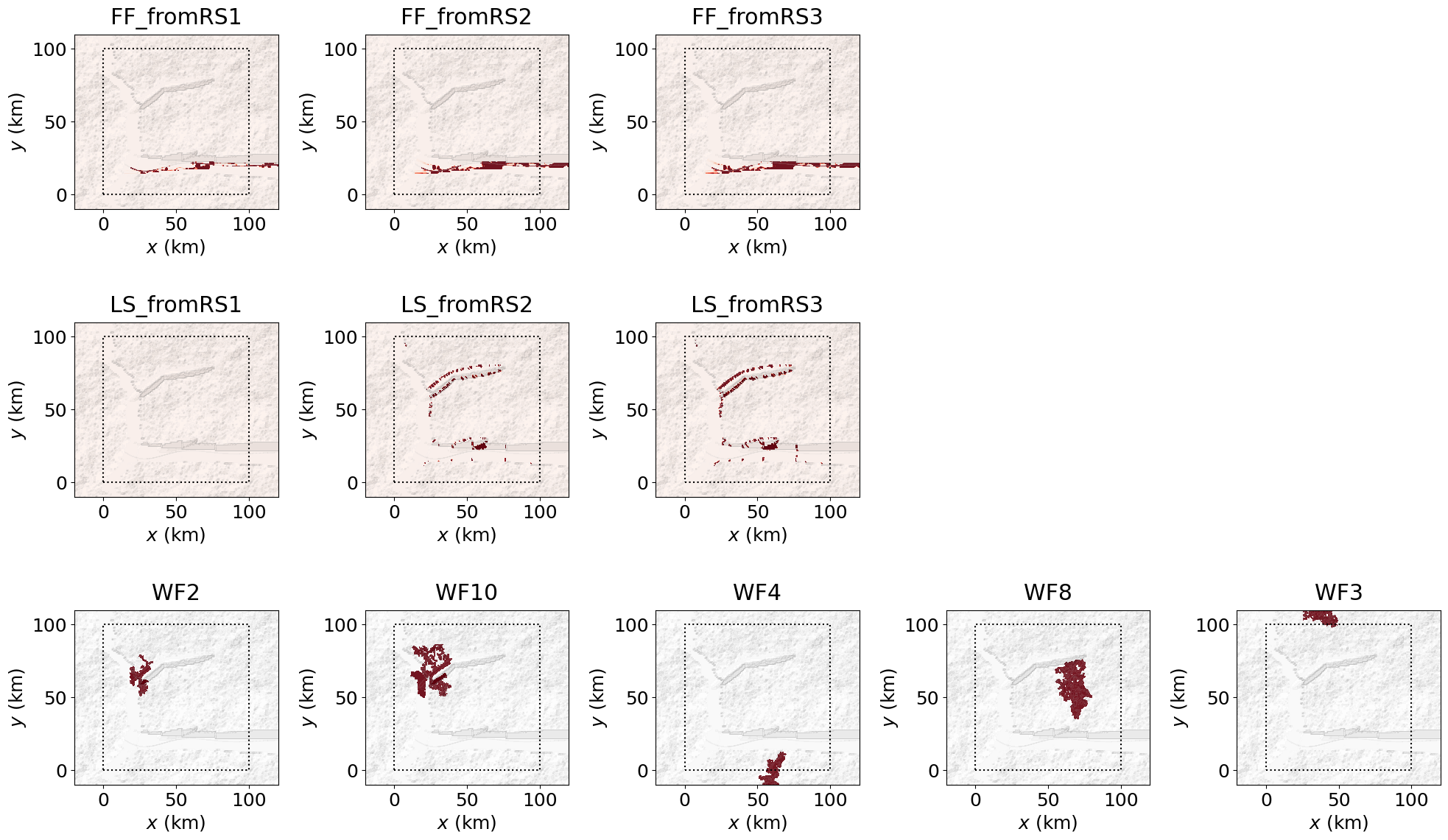
# merge the two catalogues
catalog_allhazFootprints = catalog_hazFootprints | catalog_dynhazFootprints

# bypass dynamic footprints for rapid tests...
#catalog_allhazFootprints = catalog_hazFootprints

2. Probabilistic risk assessment

In this final section, loss footprints are modelled, and total losses per event are added as new column in the event table, creating an event loss table (ELT). Risk metrics are then calculated from the ELT (considering only primary events in this tutorial). Year loss tables will be addressed in the future Tutorial 3.

2.1. Vulnerability curve definition

Generic intensity-specific vulnerability functions, \(D = f_D(I)\), are implemented and apply to any building type for simplicity. The vulnerability functions (f_D()) are listed below and correspond to the equations described in Section 3.2.5 of Mignan (2024). Damage is expressed in terms of the mean damage ratio (MDR):

ID	Intensity \(I\)	Vulnerability function	Parameters
AI, Ex	Blast overpressure \(P\) [kPa]	Cum. lognormal distr. (Eq. 3.13)	\(\mu\) = log(20), \(\sigma\) = 0.4
EQ	Peak ground acceleration PGA [m/s\(^2\)]	Cum. lognormal distr. (Eq. 3.13)	\(\mu\) = log(6), \(\sigma\) = 0.6
FF, SS	Inundation depth \(h\) [m]	Square root (Eq. 3.10)	\(c\) = 0.45
LS	Landslide thickness \(h\) [m]	Weibull distr. (Eq. 3.12)	\(c_1\) = -1.671, \(c_2\) = 3.189, \(c_3\) = 1.746
VE	Ash load \(P\) [kPa] (converted from thickness [m])	Cum. lognormal distr. (Eq. 3.13)	\(\mu\) = 1.6, \(\sigma\) = 0.4
TC, To, WS	Maximum wind speed \(v_{max}\) [m/s]	Power-law (Eq. 3.14)	\(v_{thres}\) = 25.7, \(v_{half}\) = 74.7
WF	Burnt yes/no	Heaviside step function	MDR = 1 if burnt, 0 otherwise

GenMR_perils.plot_vulnFunctions()

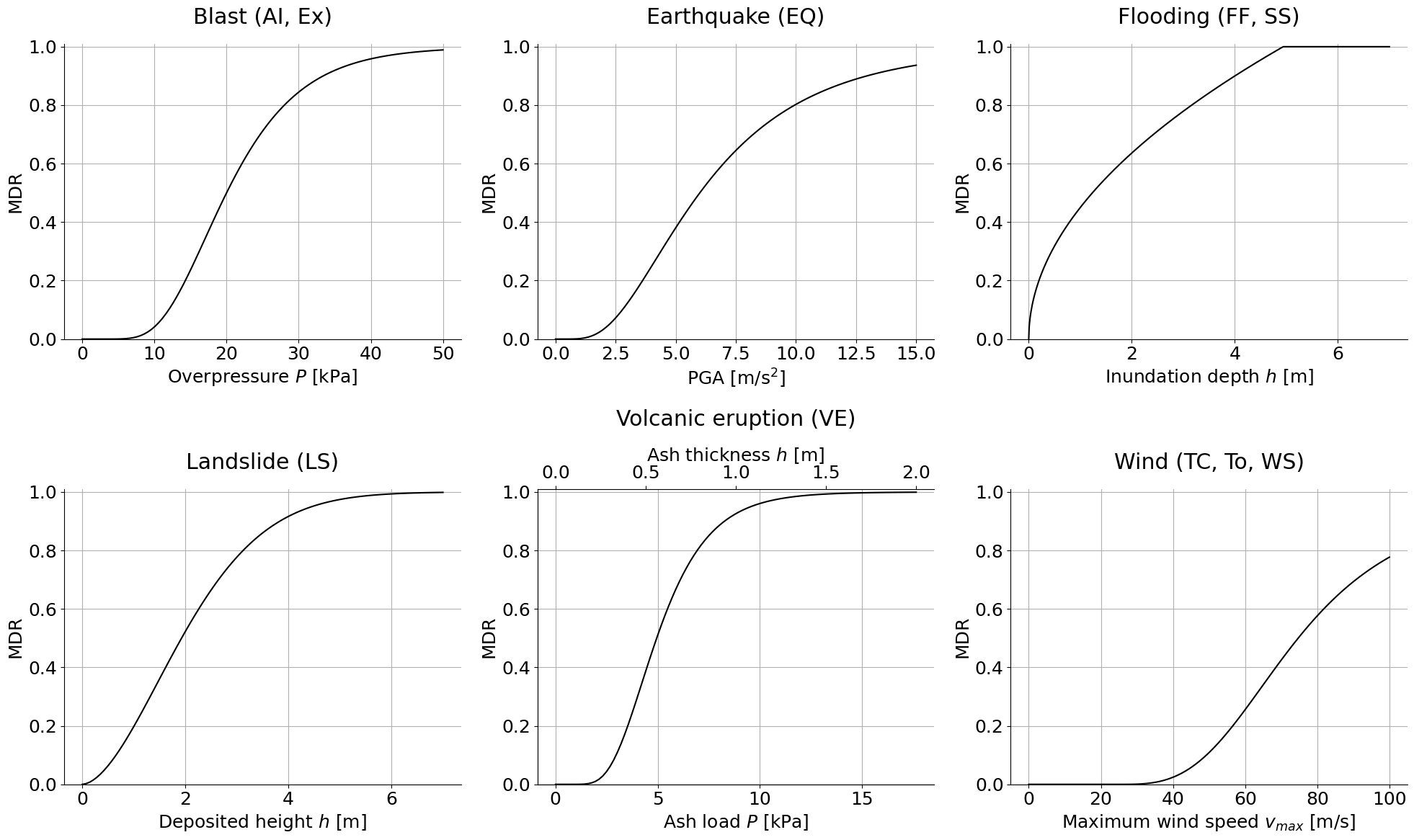
2.2. Loss footprint catalogue generation

Damage footprints, \(D(x,y)\), are obtained by mapping hazard-intensity footprints, \(I(x,y)\), into mean damage ratio (MDR) values using the vulnerability functions defined earlier. Loss footprints, \(L(x,y)\), are calculated as the product of \(D(x,y)\) and the exposure footprint, \(\nu(x,y)\).

It should be noted that losses are computed for independent events occurring individually. For example, the total loss from a TC event could depend on losses caused by the associated SS event. Such interactions, whether at the exposure or damage level, will be addressed in Tutorial 3.

riskFootprints_all = GenMR_perils.RiskFootprintGenerator(catalog_allhazFootprints, urbLandLayer, evtable)
catalog_dmgFootprints = riskFootprints_all.catalog_dmgFootprints
catalog_lossFootprints = riskFootprints_all.catalog_lossFootprints

with pd.option_context('display.max_rows', None):
    display(riskFootprints_all.ELT)

Computing MDR & Loss: 100%|█████████████████████| 76/76 [00:01<00:00, 40.31it/s]

	ID	srcID	evID	S	lbd	loss
0	AI	impact1	AI1	10.000000	2.657777e-06	1.575638e+10
1	AI	impact2	AI2	10.000000	2.657777e-06	0.000000e+00
2	AI	impact3	AI3	10.000000	2.657777e-06	2.970399e-03
3	AI	impact4	AI4	100.000000	2.509457e-07	1.732054e+05
4	AI	impact5	AI5	100.000000	2.509457e-07	1.218247e+10
5	AI	impact6	AI6	100.000000	2.509457e-07	1.321924e+10
6	AI	impact7	AI7	100.000000	2.509457e-07	1.404086e+06
7	AI	impact8	AI8	1000.000000	4.212292e-08	1.194902e+08
8	AI	impact9	AI9	1000.000000	4.212292e-08	1.131285e+11
9	AI	impact10	AI10	1000.000000	4.212292e-08	1.190284e+08
10	Dr	soil	Dr1	3.000000	NaN	NaN
11	Dr	soil	Dr2	6.000000	NaN	NaN
12	Dr	soil	Dr3	9.000000	NaN	NaN
13	EQ	fault1	EQ1	6.000000	6.855726e-03	7.495152e+08
14	EQ	fault2	EQ2	6.000000	6.855726e-03	9.030498e+09
15	EQ	fault1	EQ3	6.000000	6.855726e-03	9.566236e+07
16	EQ	fault1	EQ4	6.100000	5.445696e-03	2.092472e+08
17	EQ	fault1	EQ5	6.100000	5.445696e-03	1.778549e+07
18	EQ	fault1	EQ6	6.100000	5.445696e-03	1.037532e+09
19	EQ	fault1	EQ7	6.200000	6.488506e-03	1.277986e+09
20	EQ	fault1	EQ8	6.200000	6.488506e-03	4.576414e+07
21	EQ	fault1	EQ9	6.300000	3.436002e-03	1.768410e+09
22	EQ	fault1	EQ10	6.300000	3.436002e-03	2.302008e+08
23	EQ	fault1	EQ11	6.300000	3.436002e-03	2.302008e+08
24	EQ	fault1	EQ12	6.400000	4.093970e-03	1.012253e+09
25	EQ	fault1	EQ13	6.400000	4.093970e-03	2.672893e+09
26	EQ	fault2	EQ14	6.500000	3.251956e-03	2.800540e+10
27	EQ	fault1	EQ15	6.500000	3.251956e-03	4.604609e+08
28	EQ	fault1	EQ16	6.600000	5.166241e-03	4.156197e+09
29	EQ	fault1	EQ17	6.700000	4.103691e-03	5.561986e+09
30	EQ	fault1	EQ18	6.800000	3.259678e-03	1.579965e+09
31	EQ	fault1	EQ19	6.900000	2.589254e-03	6.052721e+09
32	EQ	fault1	EQ20	7.000000	2.056718e-03	1.055151e+10
33	HW	atmosphere	HW1	7.000000	7.400000e-04	NaN
34	HW	atmosphere	HW2	14.000000	1.700000e-04	NaN
35	HW	atmosphere	HW3	30.000000	1.000000e-05	NaN
36	PI	crops	PI1	50.000000	3.950000e-03	NaN
37	PI	crops	PI2	65.000000	0.000000e+00	NaN
38	RS	atmosphere	RS1	75.000000	1.000793e-03	NaN
39	RS	atmosphere	RS2	100.000000	8.172054e-05	NaN
40	RS	atmosphere	RS3	125.000000	4.562873e-06	NaN
41	TC	stormtrack1	TC1	40.000000	2.841439e-04	1.086326e+11
42	TC	stormtrack2	TC2	50.000000	1.637893e-04	2.164483e+11
43	TC	stormtrack3	TC3	60.000000	4.064719e-05	5.903068e+11
44	TC	stormtrack4	TC4	60.000000	4.064719e-05	8.453843e+11
45	TC	stormtrack5	TC5	70.000000	3.110718e-05	1.097077e+12
46	To	vortexline1	To1	3.000000	4.537519e-05	0.000000e+00
47	To	vortexline2	To2	3.000000	4.537519e-05	6.244221e+09
48	To	vortexline3	To3	3.000000	4.537519e-05	0.000000e+00
49	To	vortexline4	To4	4.000000	5.712399e-06	0.000000e+00
50	To	vortexline5	To5	4.000000	5.712399e-06	3.242708e+10
51	To	vortexline6	To6	4.000000	5.712399e-06	7.455413e+09
52	To	vortexline7	To7	5.000000	7.191484e-07	4.610442e+10
53	To	vortexline8	To8	5.000000	7.191484e-07	3.160345e+10
54	To	vortexline9	To9	5.000000	7.191484e-07	4.034830e+04
55	VE	volcano1	VE1	1.000000	7.303024e-07	6.178149e+02
56	VE	volcano1	VE2	3.162278	3.415881e-07	1.602683e+08
57	VE	volcano1	VE3	10.000000	1.597728e-07	6.400317e+10
58	WF	forest	WF1	10000.000000	1.062953e-02	2.415349e+09
59	WF	forest	WF2	10000.000000	1.062953e-02	2.266438e+10
60	WF	forest	WF3	10000.000000	1.062953e-02	0.000000e+00
61	WF	forest	WF4	10000.000000	1.062953e-02	0.000000e+00
62	WF	forest	WF5	10000.000000	1.062953e-02	0.000000e+00
63	WF	forest	WF6	10000.000000	1.062953e-02	0.000000e+00
64	WF	forest	WF7	31622.776602	5.158744e-03	9.154100e+10
65	WF	forest	WF8	31622.776602	5.158744e-03	7.607992e+10
66	WF	forest	WF9	31622.776602	5.158744e-03	1.918742e+10
67	WF	forest	WF10	100000.000000	3.755478e-03	4.247879e+10
68	WS	atmosphere	WS1	45.000000	2.741867e-03	1.508013e+11
69	WS	atmosphere	WS2	50.000000	1.746819e-05	2.846636e+11
70	CS	supercell	CS_toTo1	13.811900	NaN	NaN
71	CS	supercell	CS_toTo2	13.811900	NaN	NaN
72	CS	supercell	CS_toTo3	13.811900	NaN	NaN
73	CS	supercell	CS_toTo4	13.811900	NaN	NaN
74	CS	supercell	CS_toTo5	13.811900	NaN	NaN
75	CS	supercell	CS_toTo6	13.811900	NaN	NaN
76	CS	supercell	CS_toTo7	13.811900	NaN	NaN
77	CS	supercell	CS_toTo8	13.811900	NaN	NaN
78	CS	supercell	CS_toTo9	13.811900	NaN	NaN
79	Ex	refinery	Ex_fromCIf	1.000000	NaN	1.696280e+09
80	FF	river1	FF_fromRS1	NaN	NaN	2.789031e+09
81	FF	river1	FF_fromRS2	NaN	NaN	2.175961e+10
82	FF	river1	FF_fromRS3	NaN	NaN	2.647483e+10
83	Li	supercell	Li_fromCS1	NaN	NaN	NaN
84	Li	supercell	Li_fromCS2	NaN	NaN	NaN
85	Li	supercell	Li_fromCS3	NaN	NaN	NaN
86	Li	supercell	Li_fromCS4	NaN	NaN	NaN
87	Li	supercell	Li_fromCS5	NaN	NaN	NaN
88	Li	supercell	Li_fromCS6	NaN	NaN	NaN
89	Li	supercell	Li_fromCS7	NaN	NaN	NaN
90	Li	supercell	Li_fromCS8	NaN	NaN	NaN
91	Li	supercell	Li_fromCS9	NaN	NaN	NaN
92	LS	terrain	LS_fromRS1	NaN	NaN	0.000000e+00
93	LS	terrain	LS_fromRS2	NaN	NaN	8.301439e+08
94	LS	terrain	LS_fromRS3	NaN	NaN	2.189653e+09
95	SS	coastline	SS_fromTC1	NaN	NaN	3.452790e+09
96	SS	coastline	SS_fromTC2	NaN	NaN	1.184006e+10
97	SS	coastline	SS_fromTC3	NaN	NaN	2.723853e+10
98	SS	coastline	SS_fromTC4	NaN	NaN	5.868062e+10
99	SS	coastline	SS_fromTC5	NaN	NaN	7.112751e+10

nfp = len(catalog_lossFootprints)
evIDs = list(catalog_lossFootprints.keys())

mean_bldg_blockValue = np.nanmean(urbLandLayer.bldg_blockValue)
vmin = 0
vmax = .05 * mean_bldg_blockValue
levels = np.linspace(vmin, vmax, 100)

ncols = 3
nrows = int(np.ceil(nfp / ncols))
fig, ax = plt.subplots(nrows, ncols, figsize=(20, 5*nrows))
ax = ax.flatten()  

for i in range(nfp):
    loss_plt = catalog_lossFootprints[evIDs[i]].copy()
    loss_plt[loss_plt > vmax] = vmax
    ax[i].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
    ax[i].contourf(grid.xx, grid.yy, loss_plt, cmap = 'Reds', levels=levels)
    ax[i].set_xlabel('$x$ (km)')
    ax[i].set_ylabel('$y$ (km)')
    ax[i].set_title(evIDs[i])
    ax[i].set_aspect(1)

for i in range(nfp, nrows*ncols):
    ax[i].axis('off')

plt.tight_layout();

# NB: adapt event size considered and vulnerability to focus on highly damaging events only (illustrative cases)

2.3. Risk metrics

Several risk metrics are derived from the ELT, including the annual average loss (AAL), exceeding probability (EP) curves, value at risk (VaR) at a given quantile \(q\), and the tail value at risk (TVaR):

q_VAR = .99
ELT = riskFootprints_all.ELT
ELT['L'] = ELT['loss']
ELT = ELT[~np.isnan(ELT['lbd'])]   # secondary events (no rate in Tutorial 2 removed)
ELT_wEP, AAL, VaRq, TVaRq, _, _ = GenMR_utils.calc_riskmetrics_fromELT(ELT, q_VAR)

print('** from ELT **')
print('AAL [$ M.]:', AAL * 1e-6)
print('VaR_q [$ B.]:', VaRq * 1e-9)
print('TVaR_q [$ B.]:', TVaRq * 1e-9)  # much higher than VaR due to very long risk tail (default parameterisation)

plt.rcParams['font.size'] = '20'
fig, ax = plt.subplots(1,1, figsize = (20,8))
plt.scatter(ELT_wEP['L'] * 1e-9, ELT_wEP['EP'], color = 'black')
plt.plot(ELT_wEP['L'] * 1e-9, ELT_wEP['EP'], color = 'darkred')
plt.axhline(y = 1 - q_VAR, linestyle = 'dotted', color = 'black')
plt.axvline(x = VaRq * 1e-9, linestyle = 'dotted', color = 'darkred')
#plt.xlim(0,20)
#plt.ylim(0,.1)
plt.xlabel('Economic losses [$ B.]')
plt.ylabel('Exceedance probability')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False);

** from ELT **
AAL [$ M.]: 2253.0089493977466
VaR_q [$ B.]: 86.83224400803859
TVaR_q [$ B.]: 406.632526622705

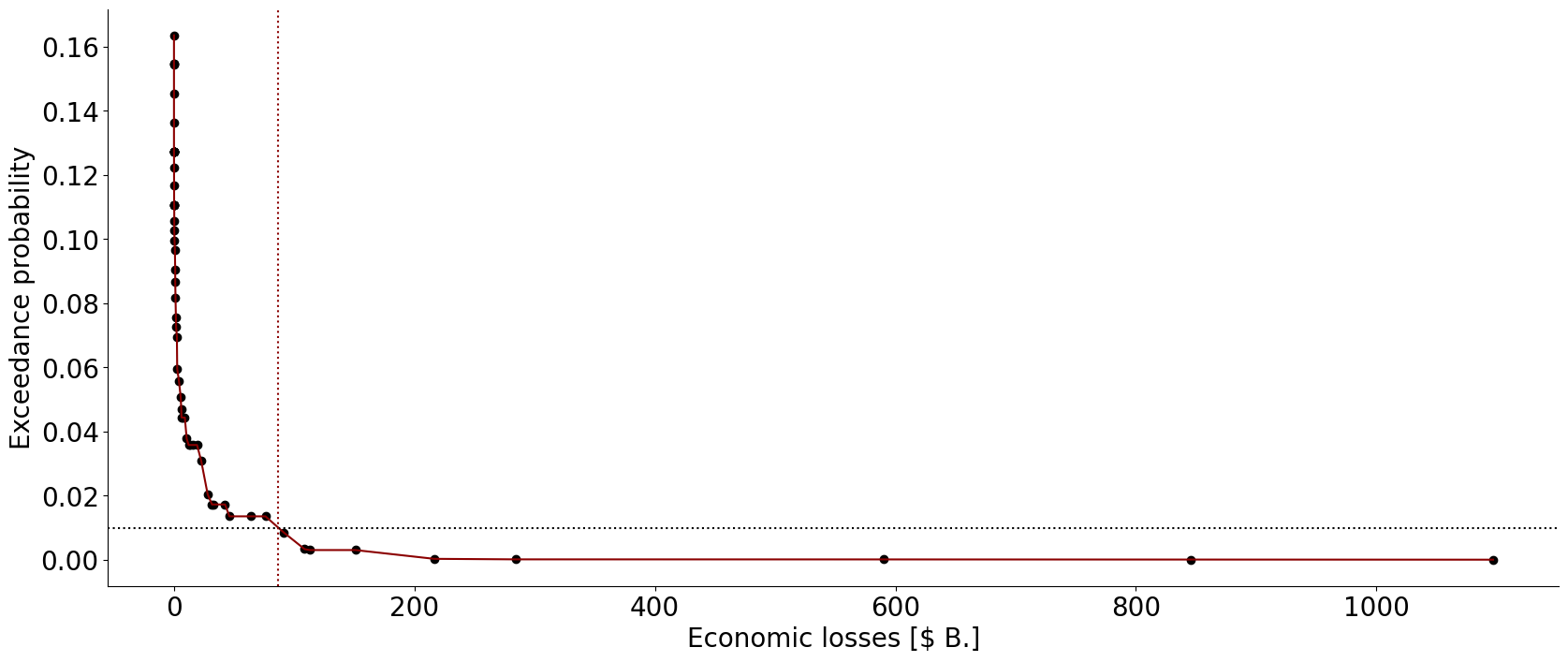
References

• Mignan A (2024), Introduction to Catastrophe Risk Modelling - A Physics-based Approach. Cambridge University Press, doi: 10.1017/9781009437370

Appendix

This appendix provides additional details that are kept outside the main notebook to maintain the clarity and flow of the main content.

A. Peril sources

Tab. A1. Full list of attributes and properties in source class src.

Attribute	ID	Description
Parameters	par	Input source parameters
Spatial grid	grid	copy of RasterGrid class
Asteroid impact source characteristics	AI_char	Stochastic point-source coordinates
Earthquake source characteristics	EQ_char	Fault source and segment coordinates, magnitudes and geometries
Fluvial flood source characteristics	FF_char	River bed coordinates
Storm surge source characteristics	SS_char	Coastline coordinates
Tropical cyclone source characteristics	TC_char	Stochastic track-source coordinates
Volcanic eruption source characteristics	VE_char	Point-source coordinates

B. Stochastic event set

B.1. Drought case

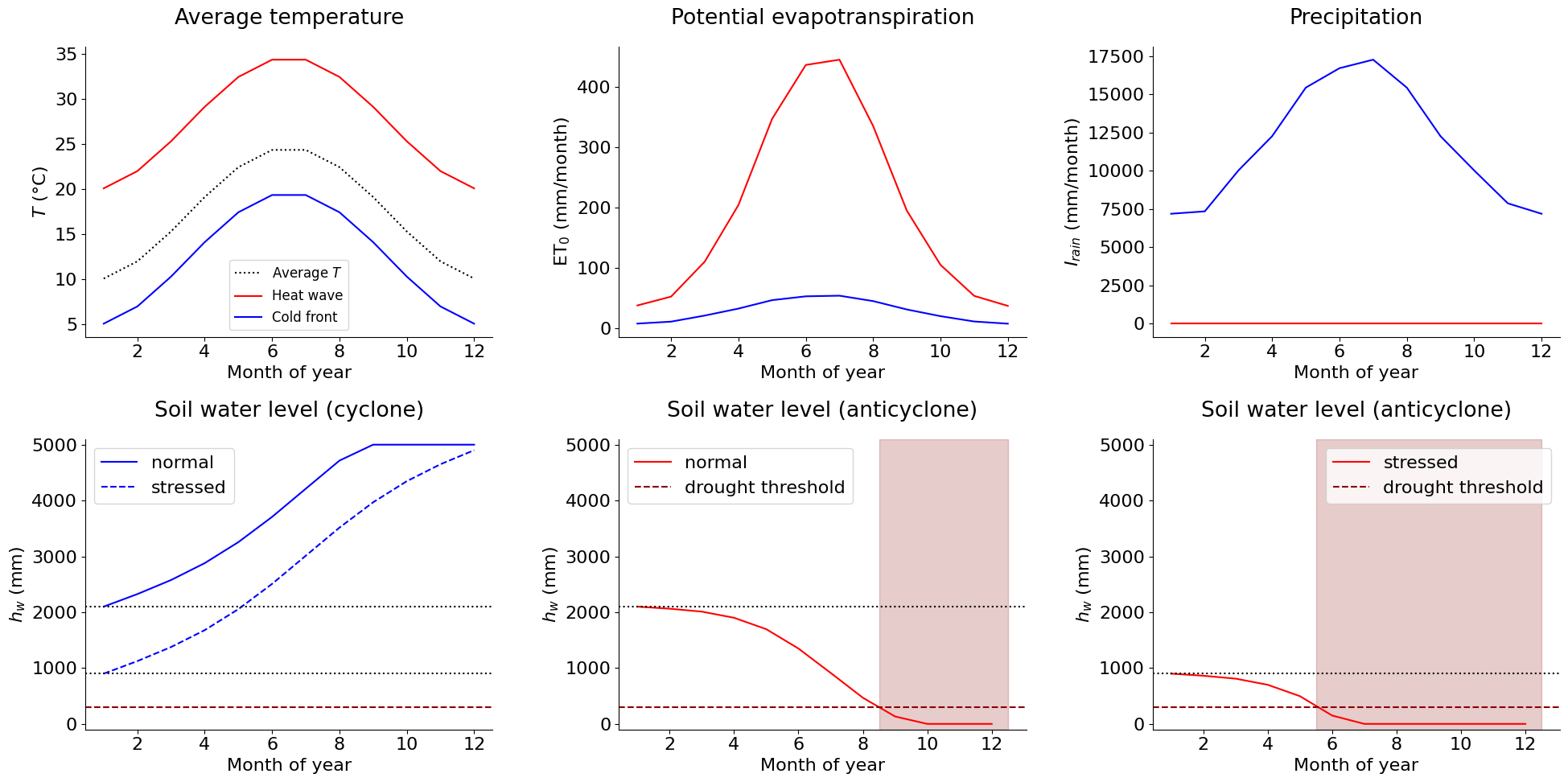
The next code cell illustrates how droughts emerge from the coupling between the atmospheric and soil layers. Four scenarios are considered: an anticyclonic regime with extreme temperatures (also characteristic of heatwaves) and a cyclonic regime (addressed in Tutorial 3 in the context of rainstorms), each evaluated under two soil water storage conditions: normal and stressed.

DTadv_anti = 10.      # anticyclone case (possible drought, heatwave)
DTadv_cycl = -5.      # cyclone case (precipitation, possible rainstorm)

moni = np.arange(12)+1
T0_mo, _, _ = GenMR_env.EnvLayer_atmo.calc_T0_EBCM(src.par['Dr']['lat_deg'], moni)   # mean monthly temperature
T_mo_anti = T0_mo + DTadv_anti       # at z = 0: extreme advection (i.e. HW potential during summer)
T_mo_cycl = T0_mo + DTadv_cycl       # at z = 0: cold front (i.e., precipitation)

## evapotranspiration from soils ##
ET0_anti = GenMR_perils.calc_PET(T_mo_anti, src.par['Dr']['lat_deg'], cloudy = False)
ET0_cycl = GenMR_perils.calc_PET(T_mo_cycl, src.par['Dr']['lat_deg'], cloudy = True)

## precipitation ##
w_anti = atmoLayer.par['vz_subs_asc'][0]      # large-scale vertical velocity (m/s), w < 0: subside (anticyclone)
w_cycl = atmoLayer.par['vz_subs_asc'][1]      # w > 0: ascent (cyclone), high amplitude in strong convection

z_tropopause = GenMR_env.EnvLayer_atmo.calc_z_tropopause(src.par['Dr']['lat_deg'])
par_rain = {'p0': atmoLayer.par['p0_kPa'], 'lapse_rate': atmoLayer.par['lapse_rate_degC/km'], \
            'eta_rain': atmoLayer.par['eta_rain'], 'zmax_km': z_tropopause}
I_rain_anti = GenMR_perils.gen_precipitation(T_mo_anti, w_anti, par_rain)
I_rain_cycl = GenMR_perils.gen_precipitation(T_mo_cycl, w_cycl, par_rain)

## soil water storage ##
Dr_th = .1                   # 10% of standard storage

hw_max = soilLayer.par['hw_max_m'] * 1000.            # (mm)
hw0_normal = .7 * soilLayer.par['hw_fc_m'] * 1000.     # well-watered soil
hw0_stress = .3 * soilLayer.par['hw_fc_m'] * 1000.     # drought-prone initial state

hw_mo_anti_normal = GenMR_perils.update_soil_moisture(I_rain_anti, ET0_anti, hw0_normal, hw_max)
hw_mo_cycl_normal = GenMR_perils.update_soil_moisture(I_rain_cycl, ET0_cycl, hw0_normal, hw_max)
hw_mo_anti_stress = GenMR_perils.update_soil_moisture(I_rain_anti, ET0_anti, hw0_stress, hw_max)
hw_mo_cycl_stress = GenMR_perils.update_soil_moisture(I_rain_cycl, ET0_cycl, hw0_stress, hw_max)

## drought emergence ##
Dr_ti_normal, Dr_S_normal = GenMR_perils.get_Dr(hw_mo_anti_normal, \
                                                soilLayer.par['hw_fc_m'] * 1000. * src.par['Dr']['hw_th'])
Dr_ti_stress, Dr_S_stress = GenMR_perils.get_Dr(hw_mo_anti_stress, \
                                                soilLayer.par['hw_fc_m'] * 1000. * src.par['Dr']['hw_th'])
print(f'In anticyclone regime, drought duration = {Dr_S_normal[0]} months in normal soil water conditions')
print(f'In anticyclone regime, drought duration = {Dr_S_stress[0]} months in stressed soil water conditions')

ndays_inMonth = GenMR_utils.get_ndays_inMonth()
plt.rcParams['font.size'] = '16'
eps = 100
fig, ax = plt.subplots(2,3, figsize=(20,10))

ax[0,0].plot(moni, T0_mo, color = 'black', linestyle = 'dotted', label = 'Average $T$')
ax[0,0].plot(moni, T_mo_anti, color = 'red', label = 'Heat wave')
ax[0,0].plot(moni, T_mo_cycl, color = 'blue', label = 'Cold front')
ax[0,0].set_xlabel('Month of year')
ax[0,0].set_ylabel('$T$ (°C)')
ax[0,0].set_title('Average temperature', pad = 20)
ax[0,0].legend(fontsize = 12)
ax[0,0].spines['right'].set_visible(False)
ax[0,0].spines['top'].set_visible(False)

ax[0,1].plot(moni, ET0_anti, color = 'red')
ax[0,1].plot(moni, ET0_cycl, color = 'blue')
ax[0,1].set_xlabel('Month of year')
ax[0,1].set_ylabel('ET$_0$ (mm/month)')
ax[0,1].set_title('Potential evapotranspiration', pad = 20)
ax[0,1].spines['right'].set_visible(False)
ax[0,1].spines['top'].set_visible(False)

ax[0,2].plot(moni, I_rain_anti * ndays_inMonth, color = 'red')
ax[0,2].plot(moni, I_rain_cycl * ndays_inMonth, color = 'blue')
ax[0,2].set_xlabel('Month of year')
ax[0,2].set_ylabel('$I_{rain}$ (mm/month)')
ax[0,2].set_title('Precipitation', pad = 20)
ax[0,2].spines['right'].set_visible(False)
ax[0,2].spines['top'].set_visible(False)

ax[1,0].plot(moni, hw_mo_cycl_normal, color = 'blue', label = 'normal')
ax[1,0].plot(moni, hw_mo_cycl_stress, color = 'blue', linestyle = 'dashed', label = 'stressed')
ax[1,0].axhline(hw0_normal, color = 'black', linestyle = 'dotted')
ax[1,0].axhline(hw0_stress, color = 'black', linestyle = 'dotted')
ax[1,0].axhline(soilLayer.par['hw_fc_m'] * 1000. * src.par['Dr']['hw_th'], color = 'darkred', linestyle = 'dashed')
ax[1,0].set_xlabel('Month of year')
ax[1,0].set_ylabel('$h_w$ (mm)')
ax[1,0].set_title('Soil water level (cyclone)', pad = 20)
ax[1,0].set_ylim(0-eps, soilLayer.par['hw_max_m'] * 1000.+eps)
ax[1,0].legend()
ax[1,0].spines['right'].set_visible(False)
ax[1,0].spines['top'].set_visible(False)

ax[1,1].plot(moni, hw_mo_anti_normal, color = 'red', label = 'normal')
ax[1,1].axhline(hw0_normal, color = 'black', linestyle = 'dotted')
ax[1,1].axhline(soilLayer.par['hw_fc_m'] * 1000. * src.par['Dr']['hw_th'], color = 'darkred', \
                linestyle = 'dashed', label = 'drought threshold')
for start, end in Dr_ti_normal:
    ax[1,1].axvspan(moni[start] - .5, moni[end] + .5, color='darkred', alpha = .2)
ax[1,1].set_xlabel('Month of year')
ax[1,1].set_ylabel('$h_w$ (mm)')
ax[1,1].set_title('Soil water level (anticyclone)', pad = 20)
ax[1,1].set_ylim(0-eps, soilLayer.par['hw_max_m'] * 1000.+eps)
ax[1,1].legend()
ax[1,1].spines['right'].set_visible(False)
ax[1,1].spines['top'].set_visible(False)

ax[1,2].plot(moni, hw_mo_anti_stress, color = 'red', label = 'stressed')
ax[1,2].axhline(hw0_stress, color = 'black', linestyle = 'dotted')
ax[1,2].axhline(soilLayer.par['hw_fc_m'] * 1000. * src.par['Dr']['hw_th'], color = 'darkred', \
                linestyle = 'dashed', label = 'drought threshold')
for start, end in Dr_ti_stress:
    ax[1,2].axvspan(moni[start] - .5, moni[end] + .5, color='darkred', alpha = .2)
ax[1,2].set_xlabel('Month of year')
ax[1,2].set_ylabel('$h_w$ (mm)')
ax[1,2].set_title('Soil water level (anticyclone)', pad = 20)
ax[1,2].set_ylim(0-eps, soilLayer.par['hw_max_m'] * 1000.+eps)
ax[1,2].legend()
ax[1,2].spines['right'].set_visible(False)
ax[1,2].spines['top'].set_visible(False)

fig.tight_layout();

In anticyclone regime, drought duration = 4 months in normal soil water conditions
In anticyclone regime, drought duration = 7 months in stressed soil water conditions

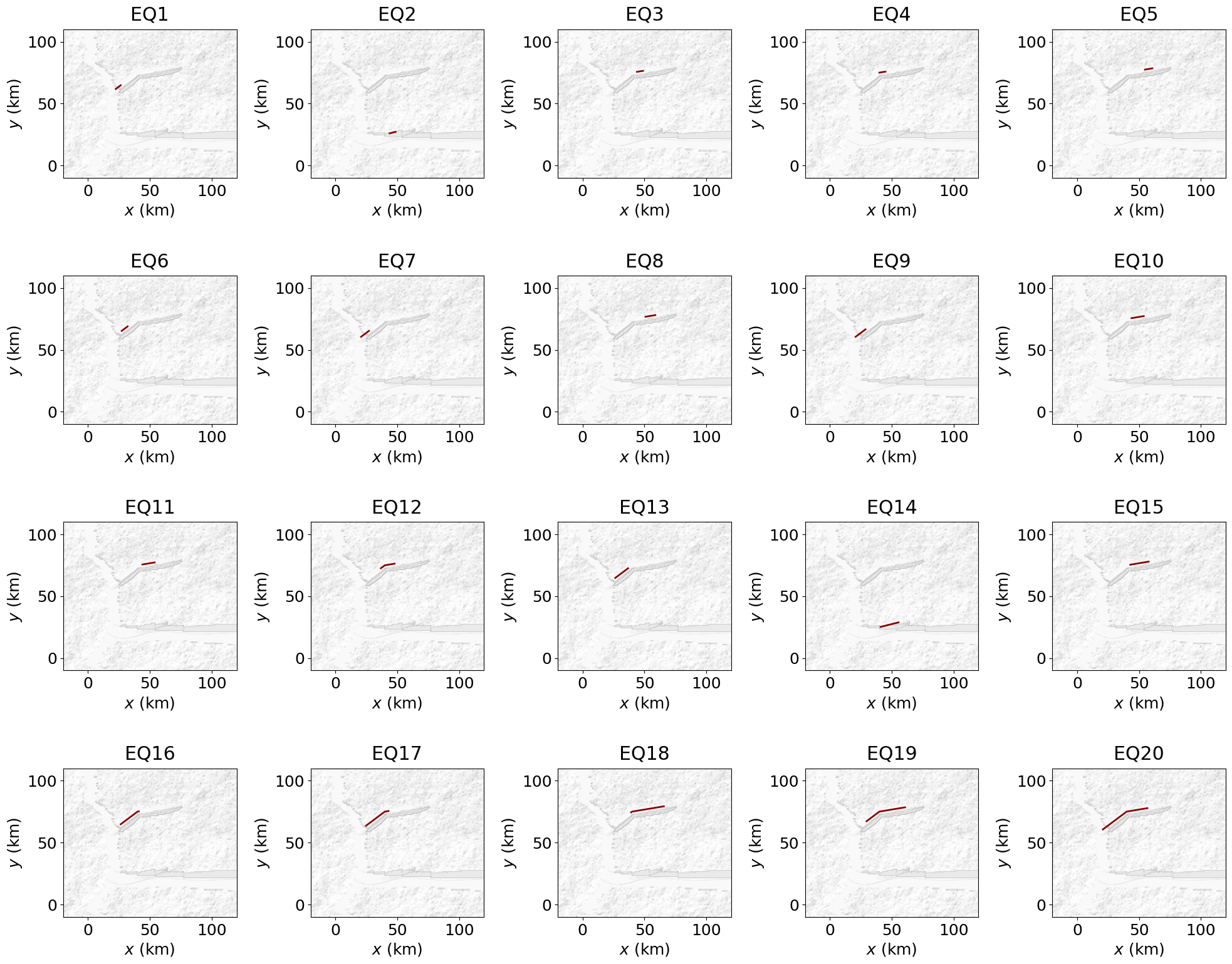
B.2. Earthquake case

The coordinates of stochastic events (defined in evchar) generally match those of their sources for localised peril sources (for diffuse sources, cellular automata are applied to determine the spatial characteristics of each event). In the case of earthquakes however, a floating rupture approach is used to generate earthquake ruptures on existing fault segments. The next cell illustrates how to extract the relevant information from evchar and how to examine the resulting spatial configuration in a stochastic run of EventSetGenerator().

EQcoord = evchar[GenMR_perils.get_peril_evID(evchar['evID']) == 'EQ'].reset_index(drop = True)
EQi = evtable[evtable['ID'] == 'EQ']['evID'].values

plt.rcParams['font.size'] = '18'
fig, ax = plt.subplots(4, 5, figsize=(20,16))
ax = ax.flatten()
for i in range(sizeDistr['EQ']['Nstoch']):
    EQcoord_evID = EQcoord[EQcoord['evID'] == EQi[i]]
    ax[i].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
    ax[i].plot(EQcoord_evID['x'], EQcoord_evID['y'], color = 'darkred', linewidth = 2)
    ax[i].set_xlim(grid.xmin, grid.xmax)
    ax[i].set_ylim(grid.ymin, grid.ymax)
    ax[i].set_xlabel('$x$ (km)')
    ax[i].set_ylabel('$y$ (km)')
    ax[i].set_title(EQi[i], pad = 10)
    ax[i].set_aspect(1)
plt.tight_layout()
plt.pause(1)   # to avoid rare case where plot not displayed on notebook
plt.show()

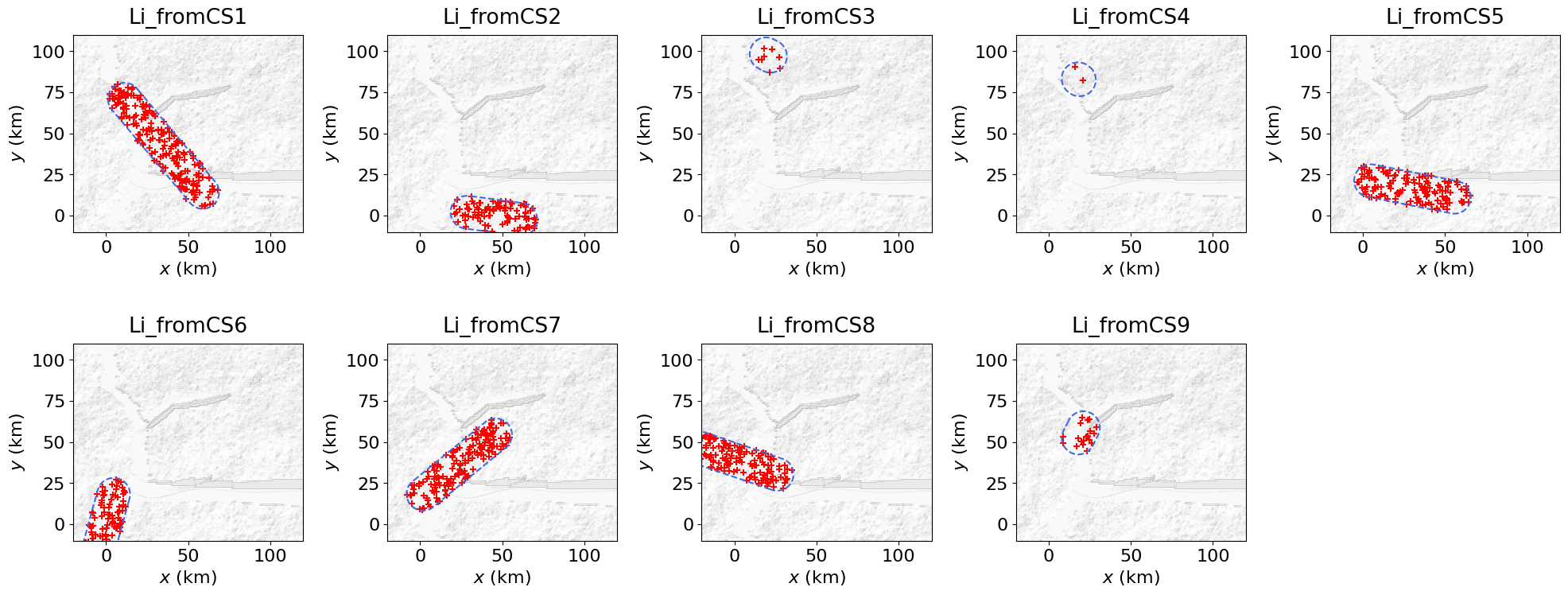
B.3. Lightning case

Lightning is triggered by convective storms. For a given CS* event, the corresponding Li_fromCS* event represents a set of lightning strikes, whose occurrence rate depends on the storm size (i.e., the cloud top height) and latitude. As shown below, lightning strikes are sampled from a spatially uniform random distribution within the storm footprint.

CS_coords = evchar[evchar['evID'].str[:2] == 'CS'].reset_index(drop = True)
Li_coords = evchar[evchar['evID'].str[:2] == 'Li'].reset_index(drop = True)
CS_list = CS_coords['evID'].unique()
Li_list = Li_coords['evID'].unique()

n_evID = len(CS_list)
max_cols = 5
ncols = min(n_evID, max_cols)
nrows = int(np.ceil(n_evID / ncols))

plt.rcParams['font.size'] = '16'
fig, ax = plt.subplots(nrows, ncols, figsize=(4 * ncols, 4 * nrows), squeeze=False)
ax = ax.flatten()
for i in range(n_evID):
    CS2plt = CS_coords[CS_coords['evID'] == CS_list[i]]
    Li2plt = Li_coords[Li_coords['evID'] == Li_list[i]]
    ax[i].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
    ax[i].plot(CS2plt['x'], CS2plt['y'], color = GenMR_utils.col_peril('CS'), linestyle = 'dashed')
    ax[i].scatter(Li2plt['x'], Li2plt['y'], color = GenMR_utils.col_peril('Li'), marker = '+')
    ax[i].set_xlim(grid.xmin, grid.xmax)
    ax[i].set_ylim(grid.ymin, grid.ymax)
    ax[i].set_xlabel('$x$ (km)')
    ax[i].set_ylabel('$y$ (km)')
    ax[i].set_title(Li_list[i], pad = 10)
    ax[i].set_aspect(1)

for j in range(n_evID, len(ax)):
    ax[j].axis('off')
    
plt.tight_layout();

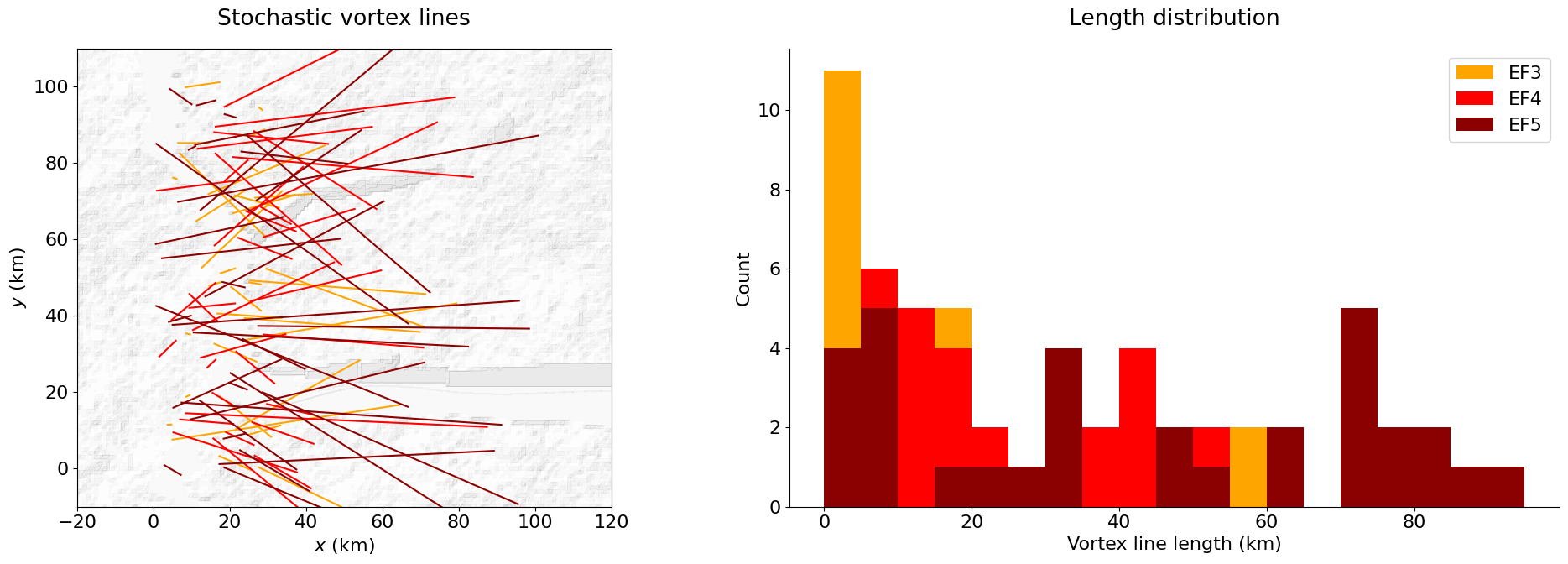
B.4. Tornado case

Change (e.g., increase) src_test.par['To']['N'] to test the stochastic properties of the tornado vortex-lines (i.e., initiation points random uniform, random strike, length according to EF-level Beta distribution).

TO IMPROVE: constrain initiation point locations (mask water mass and high altitude).

src_test = copy.deepcopy(src)
src_test.par['perils'] = ['To']
src_test.par['To']['N'] = 100
src_test.par['To']['theta_var'] = 45.
src_test.par['rdm_seed'] = None
sizeDistr_test = sizeDistr.copy()
sizeDistr_test['special'] = []     # remove 'CS'
sizeDistr_test['To']['Nstoch'] = src_test.par['To']['N']

eventSet_test = GenMR_perils.EventSetGenerator(src_test, sizeDistr_test, GenMR_utils)
evtable_test, evchar_test = eventSet_test.generate()

evchar_To = evchar_test[evchar_test['evID'].str.startswith('To')]
evIDi = evchar_To['evID'].unique()

L3 = np.array([])
L4 = np.array([])
L5 = np.array([])
plt.rcParams['font.size'] = '16'
fig, ax = plt.subplots(1,2, figsize = (20,7))
ax[0].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
for i in evIDi:
    indev = evchar_To['evID'] == i
    x_To = evchar_To[indev]['x'].values
    y_To = evchar_To[indev]['y'].values
    L = np.sqrt((x_To[-1]-x_To[0])**2 + (y_To[-1]-y_To[0])**2)
    
    if evtable_test[evtable_test['evID'] == i]['S'].values == 3:
        col = 'orange'
        L3 = np.append(L3, L)
    elif evtable_test[evtable_test['evID'] == i]['S'].values == 4:
        col = 'red'
        L4 = np.append(L4, L)
    else:
        col = 'darkred'
        L5 = np.append(L5, L)
    ax[0].plot(x_To, y_To, color = col)

ax[0].set_xlim(grid.xmin, grid.xmax)
ax[0].set_ylim(grid.ymin, grid.ymax)
ax[0].set_xlabel('$x$ (km)')
ax[0].set_ylabel('$y$ (km)')
ax[0].set_title('Stochastic vortex lines', pad = 20)
ax[0].set_aspect(1)

bins = np.arange(0, src.par['To']['L_alpha_beta_Lmax_EF3'][2], 5)
ax[1].hist(L3, bins = bins, color = 'orange', label = 'EF3')
ax[1].hist(L4, bins = bins, color = 'red', label = 'EF4')
ax[1].hist(L5, bins = bins, color = 'darkred', label = 'EF5')
ax[1].set_xlabel('Vortex line length (km)')
ax[1].set_ylabel('Count')
ax[1].set_title('Length distribution', pad = 20)
ax[1].spines['right'].set_visible(False)
ax[1].spines['top'].set_visible(False)
ax[1].legend()

fig.tight_layout();

C. Hazard footprints

C.1. Tropical cyclone case

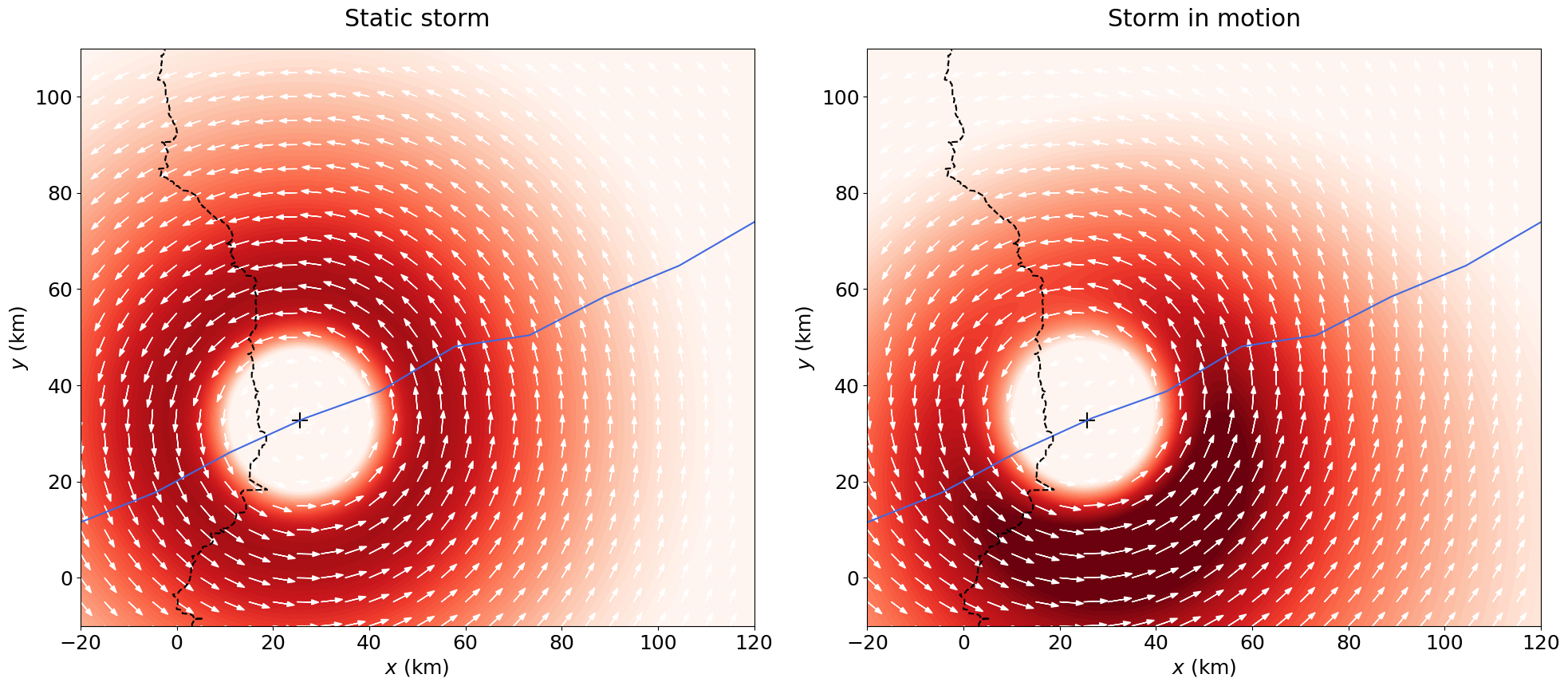
While modelling the AI, EQ, and VE intensity footprints from analytical expressions (Sect. 1.3.1) is straightforward, this is not the case for the TC peril, which involves a time-dependent intensity field. First, because the footprint depends on a moving track, a hazard-intensity field must be computed at each time increment, and the final static footprint is then defined as \(\max_t I(x,y,t)\). Second, the windfield is composed of several components, a tangential wind vector and the storm’s forward-motion vector, that must be combined to obtain the total wind amplitude. For illustration, intensity footprints at a given instant \(t\) are displayed below, together with their associated windfields, shown both without and with the effect of storm forward motion.

evID = 'TC5'     # choose a TC event
loc_x = 25.      # location of time snapshot (km)


track_evID = evchar[evchar['evID'] == evID]
t_snapshot = np.where(track_evID['x'] > loc_x)[0][0]

I_sym_t, I_asym_t, vtot_x, vtot_y, vtan_x, vtan_y = hazFootprints.get_TC_timeshot(evID, t_snapshot)


plt.rcParams['font.size'] = '18'
fig, ax = plt.subplots(1, 2, figsize=(20,10))

Imax = plot_Imax['TC']
I_plt = np.copy(I_sym_t)
I_plt[I_plt >= Imax] = Imax
ax[0].contourf(grid.xx, grid.yy, I_plt, cmap = 'Reds', levels = np.linspace(0, Imax, 100), vmin=33, vmax=Imax)
ax[0].plot(track_evID['x'], track_evID['y'], color = GenMR_utils.col_peril('TC'))
ax[0].plot(src.SS_char['x'], src.SS_char['y'], color = 'black', linestyle = 'dashed')
ax[0].scatter(track_evID['x'].values[t_snapshot], track_evID['y'].values[t_snapshot], marker = '+', \
              color = 'black', s = 200)
delta = 50
for i in range(int(grid.xx.shape[0]/delta)):
    for j in range(int(grid.xx.shape[1]/delta)):
        ax[0].arrow(grid.xx[delta*i,delta*j], grid.yy[delta*i,delta*j], 
            .05 * vtan_x[delta*i,delta*j], .05* vtan_y[delta*i,delta*j], head_width = 1, color = 'white')
ax[0].set_xlabel('$x$ (km)')
ax[0].set_ylabel('$y$ (km)')
ax[0].set_title('Static storm', pad = 20)
ax[0].set_xlim(grid.xmin, grid.xmax)
ax[0].set_ylim(grid.ymin, grid.ymax)
ax[0].set_aspect(1)

I_plt = np.copy(I_asym_t)
I_plt[I_plt >= Imax] = Imax
ax[1].contourf(grid.xx, grid.yy, I_plt, cmap = 'Reds', levels = np.linspace(0, Imax, 100), vmin=33, vmax=Imax)
ax[1].plot(track_evID['x'], track_evID['y'], color = GenMR_utils.col_peril('TC'))
ax[1].plot(src.SS_char['x'], src.SS_char['y'], color = 'black', linestyle = 'dashed')
ax[1].scatter(track_evID['x'].values[t_snapshot], track_evID['y'].values[t_snapshot], marker = '+', \
              color = 'black', s = 200)
delta = 50
for i in range(int(grid.xx.shape[0]/delta)):
    for j in range(int(grid.xx.shape[1]/delta)):
        ax[1].arrow(grid.xx[delta*i,delta*j], grid.yy[delta*i,delta*j], 
            .05 * vtot_x[delta*i,delta*j], .05* vtot_y[delta*i,delta*j], head_width = 1, color = 'white')
ax[1].set_xlabel('$x$ (km)')
ax[1].set_ylabel('$y$ (km)')
ax[1].set_title('Storm in motion', pad = 20)
ax[1].set_xlim(grid.xmin, grid.xmax)
ax[1].set_ylim(grid.ymin, grid.ymax)
ax[1].set_aspect(1)
plt.tight_layout();

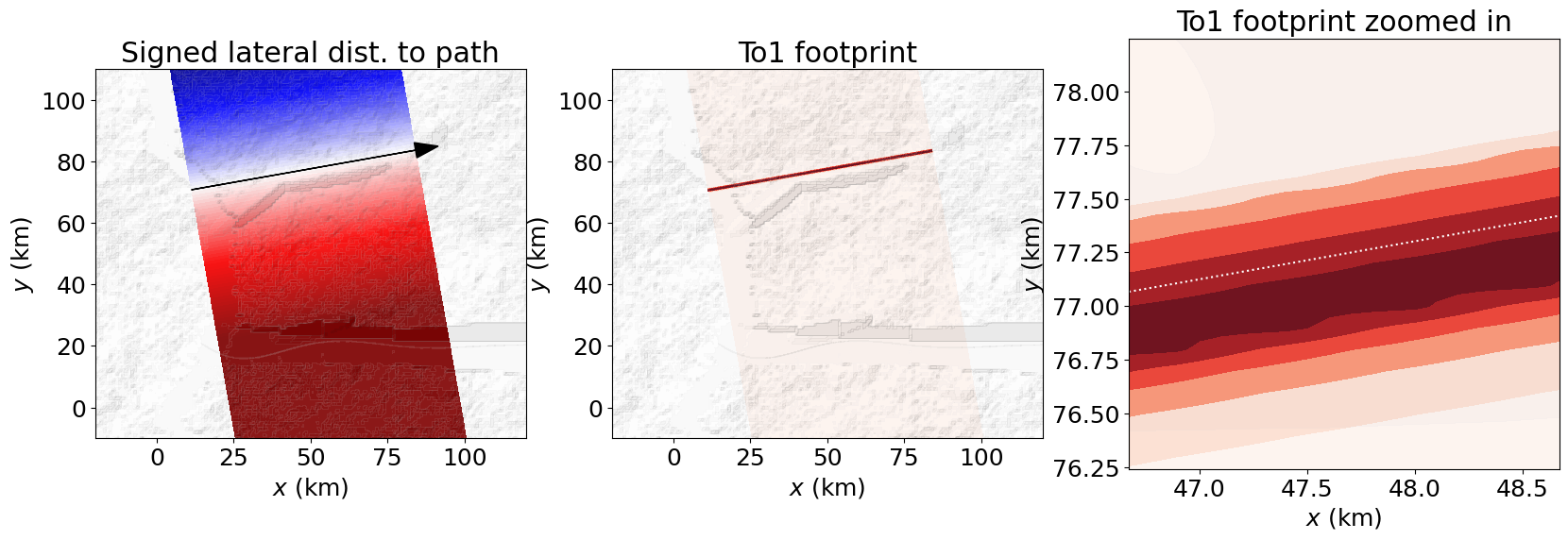
C.2. Tornado case

Since tornado intensity footprints appear as linear features at the digital template scale, the following cell zooms into a segment of a maximum wind-speed footprint to illustrate the lateral asymmetry of the wind field perpendicular to the source line.

evID = 'To1'

To_coord = evchar[evchar['evID'] == evID].reset_index(drop=True)
vmax = catalog_hazFootprints[evID]
# add signed lateral distance
r2To = GenMR_perils.HazardFootprintGenerator.calc_lateral_distance_signed(grid.xx, grid.yy, To_coord['x'], To_coord['y'])


plt.rcParams['font.size'] = '18'
fig, ax = plt.subplots(1,3, figsize = (20,7))
ax[0].contourf(grid.xx, grid.yy, r2To, cmap = 'seismic', vmin = -50, vmax = 50, levels = np.linspace(-100, 100, 201))
ax[0].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
dx = To_coord['x'].values[-1] - To_coord['x'].values[0]
dy = To_coord['y'].values[-1] - To_coord['y'].values[0]
ax[0].arrow(To_coord['x'][0], To_coord['y'][0], dx, dy, color = 'black', head_width = 5)
ax[0].set_xlim(grid.xmin, grid.xmax)
ax[0].set_ylim(grid.ymin, grid.ymax)
ax[0].set_xlabel('$x$ (km)')
ax[0].set_ylabel('$y$ (km)')
ax[0].set_title('Signed lateral dist. to path')
ax[0].set_aspect(1)

ax[1].contourf(grid.xx, grid.yy, vmax, cmap = 'Reds', vmin = 40, vmax = 80)
ax[1].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
ax[1].set_xlim(grid.xmin, grid.xmax)
ax[1].set_ylim(grid.ymin, grid.ymax)
ax[1].set_xlabel('$x$ (km)')
ax[1].set_ylabel('$y$ (km)')
ax[1].set_title(f'{evID} footprint')
ax[1].set_aspect(1)

To_x0, To_y0 = To_coord['x'].mean(), To_coord['y'].mean()
dxy = 1.  # km on each side of (x0,y0)
ax[2].contourf(grid.xx, grid.yy, vmax, cmap = 'Reds', vmin = 40, vmax = 80)
ax[2].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray', alpha = .1)
ax[2].plot(To_coord['x'], To_coord['y'], color = 'white', linestyle = 'dotted')
ax[2].set_xlim(To_x0-dxy, To_x0+dxy)
ax[2].set_ylim(To_y0-dxy, To_y0+dxy)
ax[2].set_xlabel('$x$ (km)')
ax[2].set_ylabel('$y$ (km)')
ax[2].set_title(f'{evID} footprint zoomed in')
ax[2].set_aspect(1);

C.3. Heatwave case (threshold model)

Heatwave HW temperature footprints are generated using a threshold-based model, in which an event is declared when the temperature equals or exceeds T_th for at least Dt_da consecutive days. Temperature extremes in the digital template arise from the combination of large-scale advective temperature anomalies and temporally correlated daily temperature variability.

The parameter nsig can be adjusted to explore different levels of heatwave extremity within the digital template.

from scipy.stats import norm

nsig = 3                                       # mean temperature extreme observed at nsigma
rdm_seed = 4                                   # None or integer - to test different daily fluctuations
Tmin, Tmax = 10, 40                            # range considered
month = 7

T_th = src.par['HW']['T_th']
Dt = src.par['HW']['Dt_da']
sigmaT_yearly =src.par['HW']['sigmaT_yearly']
sigmaT_daily = src.par['HW']['sigmaT_daily']
corrT = src.par['HW']['corrT']
Ndays = src.par['HW']['Dt_max_da']
dayi = np.arange(src.par['HW']['Dt_max_da'])+1
lat = grid.par['lat_deg']

Ti = np.arange(Tmin, Tmax, 1)
T0 = np.max(atmoLayer.T)                       # digital template near-surface air temperature f(lat, month)
Tnorm_pdf = norm.pdf(Ti, T0, sigmaT_yearly)    # annual variations of mean temperature

# advection model (3-Gaussian model)
Tadv_pdf, Tadv_sigma, advection_comp = GenMR_perils.HazardFootprintGenerator.pdf_T_advectivemodel(Ti, T0, lat)

Tadv_nsig = T0 + nsig * Tadv_sigma             # nsigma advective event
                                               # note: the stochastic version also includes sigmaT_yearly role
# temperature daily variations over Ndays
Tdaily_stoch_nsig = GenMR_perils.HazardFootprintGenerator.sample_T_daily(Tadv_nsig, \
                                 sigmaT_daily, Ndays = Ndays, rho = corrT, seed = rdm_seed)

print(f'T0={T0:.1f}°C, {nsig}sigma={Tadv_nsig:.1f}°C, daily max={np.max(Tdaily_stoch_nsig):.1f}°C')

# extract heatwave events according to time series only (loc where T = Tdaily_stoch_nsig)
HW_ti_nsig, HW_Dt_nsig = GenMR_perils.HazardFootprintGenerator.get_HW_atloc(Tdaily_stoch_nsig, T_th, Dt)

# define nsigma HW footprint
DTadv_nsig = Tadv_nsig - T0                          # advection shift
Tmap_mean = atmoLayer.T[month-1,:,:] + DTadv_nsig    # mean temp. map of the nsigma day, before daily fluctuations
DTdaily_stoch = Tdaily_stoch_nsig - Tadv_nsig        # daily fluctuations

nx, ny = Tmap_mean.shape
Tmap_daily_stoch = np.empty((Ndays, nx, ny))
for t in range(Ndays):
     Tmap_daily_stoch[t] = Tmap_mean + DTdaily_stoch[t]
HW_fp, HW_S = GenMR_perils.HazardFootprintGenerator.get_HW_footprint(Tmap_daily_stoch, Tth=T_th, Dt=Dt)


plt.rcParams['font.size'] = '16'
fig, ax = plt.subplots(2,4, figsize=(20,10))

ax[0,0].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
img = ax[0,0].contourf(grid.xx, grid.yy, atmoLayer.T[month-1,:,:], cmap = 'bwr', vmin=0, vmax=30, alpha = .5)
ax[0,0].set_xlabel('$x$ (km)')
ax[0,0].set_ylabel('$y$ (km)')
ax[0,0].set_title('Average temperature', pad = 20)
ax[0,0].set_aspect(1)
fig.colorbar(img, ax = ax[0,0], fraction = .04, pad = .04, label = 'Temperature (°C)')

ax[0,1].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
img = ax[0,1].contourf(grid.xx, grid.yy, atmoLayer.T[month-1,:,:] + nsig * Tadv_sigma, cmap = 'bwr', \
                 vmin=0, vmax=30, alpha = .5)
ax[0,1].set_xlabel('$x$ (km)')
ax[0,1].set_ylabel('$y$ (km)')
ax[0,1].set_title(f'Advection temp. at {nsig}$\sigma$', pad = 20)
ax[0,1].set_aspect(1)
fig.colorbar(img, ax = ax[0,1], fraction = .04, pad = .04, label = 'Temperature (°C)')

ax[0,2].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
img = ax[0,2].contourf(grid.xx, grid.yy, atmoLayer.T[month-1,:,:] + DTadv_nsig + np.max(DTdaily_stoch), \
                       cmap = 'bwr', vmin=0, vmax=30, alpha = .5)
ax[0,2].set_xlabel('$x$ (km)')
ax[0,2].set_ylabel('$y$ (km)')
ax[0,2].set_title(f'Max. daily temp. at {nsig}$\sigma$', pad = 20)
ax[0,2].set_aspect(1)
fig.colorbar(img, ax = ax[0,2], fraction = .04, pad = .04, label = 'Temperature (°C)')

ax[0,3].axis('off')


ax[1,0].plot(Ti, Tnorm_pdf, color='black')
ax[1,0].axvline(T0, color = 'black', linestyle = 'dashed', label = '$T_0$')
ax[1,0].axvline(T0 + nsig * sigmaT_yearly, color = 'black', linestyle = 'dotted', label = f'$T_0+{nsig}\sigma$')
ax[1,0].axvline(T_th, color = 'darkred', linestyle = 'dashed', label = '$T_{th}$')
ax[1,0].set_xlabel('$T$ (°C)')
ax[1,0].set_ylabel('Density')
ax[1,0].set_title('Baseline', pad = 20)
ax[1,0].spines['right'].set_visible(False)
ax[1,0].spines['top'].set_visible(False)
ax[1,0].legend(fontsize = 12)

ax[1,1].plot(Ti, advection_comp['pdf0'], color='green', linestyle = 'dashed', label = 'baseline')
ax[1,1].plot(Ti, advection_comp['pdf_c'], color='blue', linestyle = 'dashed', label = 'cold flux')
ax[1,1].plot(Ti, advection_comp['pdf_w'], color='red', linestyle = 'dashed', label = 'warm flux')
ax[1,1].plot(Ti, Tadv_pdf, color='black')
ax[1,1].axvline(T0, color = 'black', linestyle = 'dashed')
ax[1,1].axvline(Tadv_nsig, color = 'black', linestyle = 'dotted')
ax[1,1].axvline(T_th, color = 'darkred', linestyle = 'dashed')
ax[1,1].set_xlabel('$T$ (°C)')
ax[1,1].set_ylabel('Density')
ax[1,1].set_title('Advection', pad = 20)
ax[1,1].spines['right'].set_visible(False)
ax[1,1].spines['top'].set_visible(False)
ax[1,1].legend(fontsize = 12)

dayi = np.arange(Ndays)+1
ax[1,2].plot(dayi, Tdaily_stoch_nsig, color = 'black')
for start, end in HW_ti_nsig:
    ax[1,2].axvspan(dayi[start] - .5, dayi[end] + .5, color='darkred', alpha = .2)
ax[1,2].axhline(Tadv_nsig, color = 'black', linestyle = 'dotted')
ax[1,2].axhline(T_th, color = 'darkred', linestyle = 'dashed')
ax[1,2].set_ylim(T_th-5, T_th+5)
ax[1,2].set_xlabel('Day of the month')
ax[1,2].set_ylabel('$T$ (°C)')
ax[1,2].set_title(f'Daily temp. at +{nsig}$\sigma$={Tadv_nsig:.1f}°C', pad = 20)
ax[1,2].spines['right'].set_visible(False)
ax[1,2].spines['top'].set_visible(False)

ax[1,3].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
ax[1,3].contourf(grid.xx, grid.yy, HW_fp, cmap = 'Reds', alpha = .5)
ax[1,3].set_xlabel('$x$ (km)')
ax[1,3].set_ylabel('$y$ (km)')
ax[1,3].set_title(f'{nsig}$\sigma$ heatwave fp. ({HW_S} da)', pad = 20)
ax[1,3].set_aspect(1)

plt.tight_layout();

T0=24.4°C, 3sigma=34.3°C, daily max=37.8°C

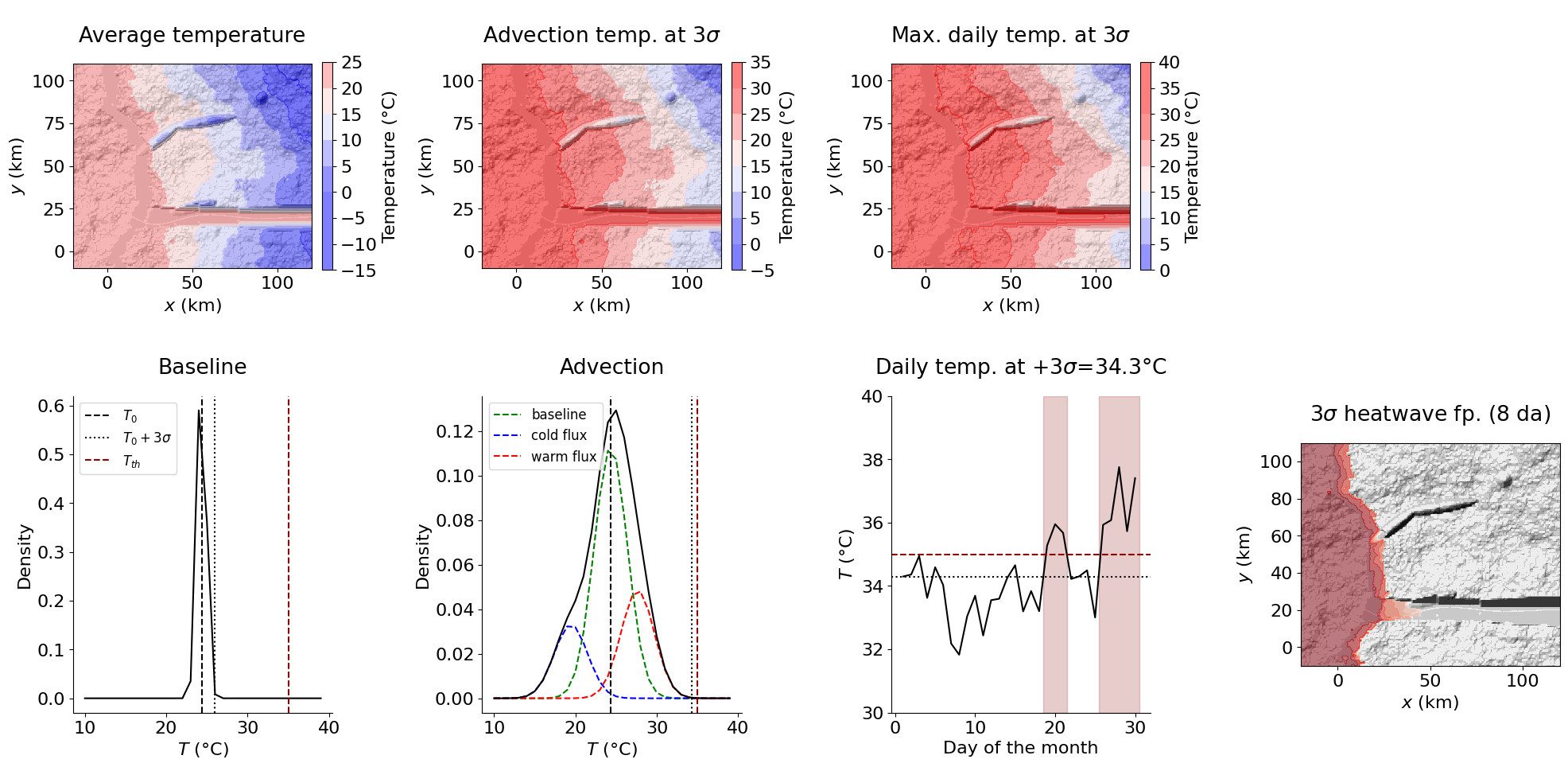
C.4. Pest infestation case

Pest infestation (PI) intensity is modelled analytically. Based on the temperature-dependent development rate of the pest (here Spodoptera frugiperda, see calc_PI_growthrate()), the hazard intensity is defined as a unitless index representing the expected number of pest larvae after one month (on the fixed time scale considered in Tutorial 2), normalised by the corresponding number at the optimal growth temperature \(T_{opt}\) (see calc_PI_I()). Consequently, at the optimal temperature the intensity equals 1, corresponding to 100% yield loss for crops located at \(T(x,y) = T_{opt}\). The resulting footprint is defined only over crop locations.

DTadv = 15    # change this value to explore impact of high temperatures relative to average temperature for July
              # DTadv represents the temperature increase from advection during heat wave


Ti = np.arange(0, 50, .1)
growrate_pest_i = GenMR_perils.HazardFootprintGenerator.calc_PI_growthrate(Ti, 'Shi')  # see other models in func.
haz_index_i, Topt = GenMR_perils.HazardFootprintGenerator.calc_PI_I(Ti, 'Shi')

month = 7
T_map = atmoLayer.T[month-1,:,:] + DTadv
haz_index_map, _ = GenMR_perils.HazardFootprintGenerator.calc_PI_I(T_map, 'Shi')
mask_crop = urbLandLayer.S >= 5

PI_fp = haz_index_map * mask_crop.astype(int)
PI_fp[PI_fp == 0] = np.nan

plt.rcParams['font.size'] = '16'
fig, ax = plt.subplots(1,3, figsize=(20,6))

ax[0].plot(Ti, growrate_pest_i, color = 'black')
ax[0].set_xlabel('$T$ (°C)')
ax[0].set_ylabel('Growth rate (/day)')
ax[0].set_title('Pest growth function', pad = 20)
ax[0].legend()
ax[0].spines['right'].set_visible(False)
ax[0].spines['top'].set_visible(False)

ax[1].plot(Ti, haz_index_i, color = 'black', label = 'hazard index')
ax[1].axvline(Topt, color = 'black', linestyle = 'dotted', label = "pest's $T_{opt}$")
ax[1].axvline(np.max(T_map), color = 'black', linestyle = 'dashed', label = "region's max. $T$")
ax[1].set_xlabel('$T$ (°C)')
ax[1].set_ylabel('Severity index (yield loss ratio)')
ax[1].set_title('Pest severity', pad = 20)
ax[1].legend()
ax[1].spines['right'].set_visible(False)
ax[1].spines['top'].set_visible(False)

S_map = int(np.nanmean(PI_fp) * 100)

ax[2].contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
ax[2].contourf(grid.xx, grid.yy, PI_fp, cmap = 'Reds', vmin=0, vmax=1, alpha = .5)
ax[2].set_xlabel('$x$ (km)')
ax[2].set_ylabel('$y$ (km)')
ax[2].set_title(f'PI footprint: mean yield reduction = {S_map}%', pad = 20)
ax[2].set_aspect(1)

plt.tight_layout();