Tutorial 1: Generating a virtual environment for the GenMR digital template

Author: Arnaud Mignan, Mignan Risk Analytics GmbH
Version: 1.1.2
Last Updated: 2026-02-12
License: AGPL-3

The digital template, first described in Mignan (2022) and used in the CAT Risk Modelling Sandbox (Mignan, 2024), is a microcosm simulation of the complex Earth system for catastrophe dynamics R&D, multi-risk prototyping in the Generic Multi-Risk (GenMR) framework, and catastrophe risk eduction. It is defined as a virtual environment populated by loss-generating events that interact with each other and with the environment. The virtual environment, to be built in this tutorial, is composed of environmental layers that consist of sets of variables \(\theta(x,y)\) defined in a spatial grid of coordinates \((x,y)\). Each layer may be altered by environmental objects located within the layer. The parsimonious complex Earth system finally consists of a stack of interacting environmental layers defined in the natural, technological and socio-economic systems. The loss-generating events that populate the virtual environment will be defined in the next tutorial, and their occurrence rates and interactions in a third and final tutorial.

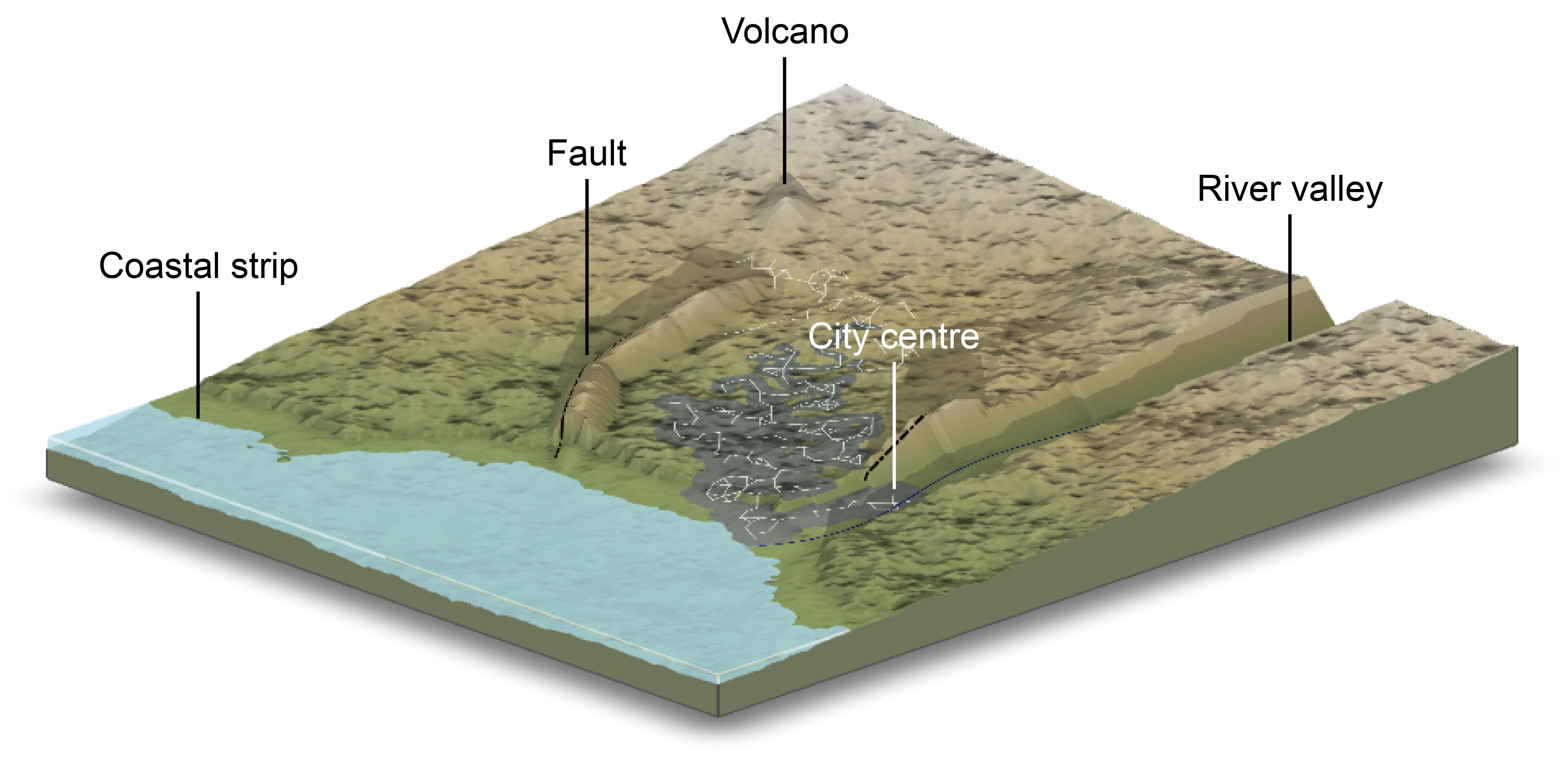
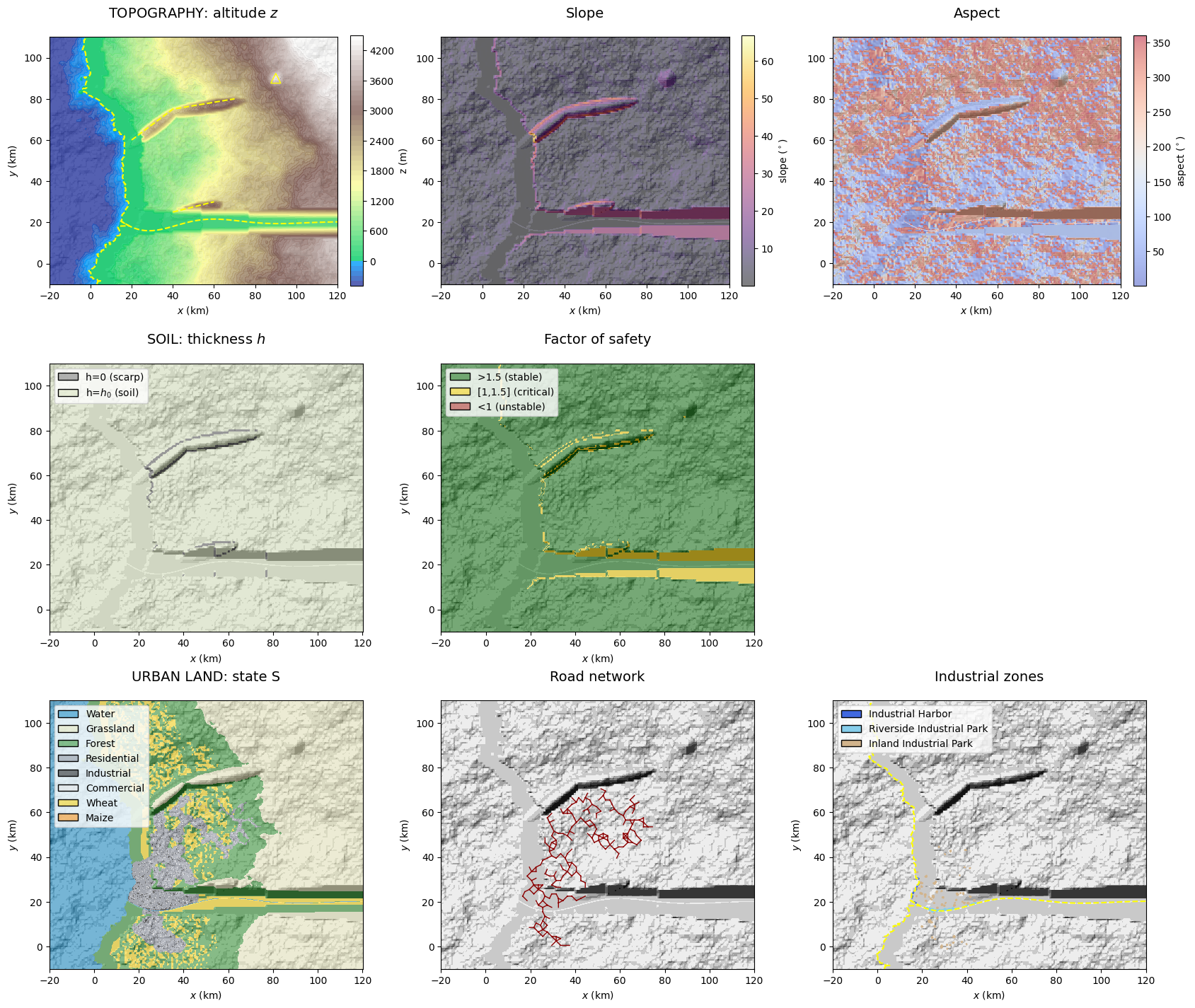
The modelled environmental layers and associated objects as listed in Table 1 (see also Fig. 1). This tutorial provides a concise overview of these layers using a default parameterisation, with alternative scenarios to be introduced later in How-To Guides. The outputs generated here will serve as input for hazard and risk assessment in the subsequent tutorials.

Tab. 1. List of environmental layers EnvLayer_ID (Python classes). See Tab. A1 for the complete list of their attributes and properties.

Environment	ID	Layer	Main variable	Properties (examples)	Object dependencies\(^*\)	References	Status‡
Natural	topo	Topography	Elevation \(z\)	Slope, aspect	Geological & hydrological objects	Mignan (2022)	✓
Natural	atmo	Atmosphere	Temperature \(T\)	Freezing level	-	N/A	✓
Natural	soil	Soil	Depth \(h\)	Factor of safety	-	Mignan (2022)	✓
Natural	natLand	Natural land	State \(S\)	-	-	Mignan (2024)	✓
Technological	urbLand	Urban (& rural) land	State \(S\)	Exposure value	Road network	Mignan (2024)	✓
Technological	energyCI	Energy infrastructures			Power grid	N/A	✗
Socio-economic	pop	Population				N/A	✗

* Each layer additionally depends on the previous ones.
^‡ Included in current version (✓), planned for v.1.1.2 (✗).

Fig. 1. The GenMR digital template (here with default parameterisation) showing the built areas in grey and road network in white. Simulation rendered using Rayshader (Morgan-Wall, 2022).
The environmental layers are generated as follows:

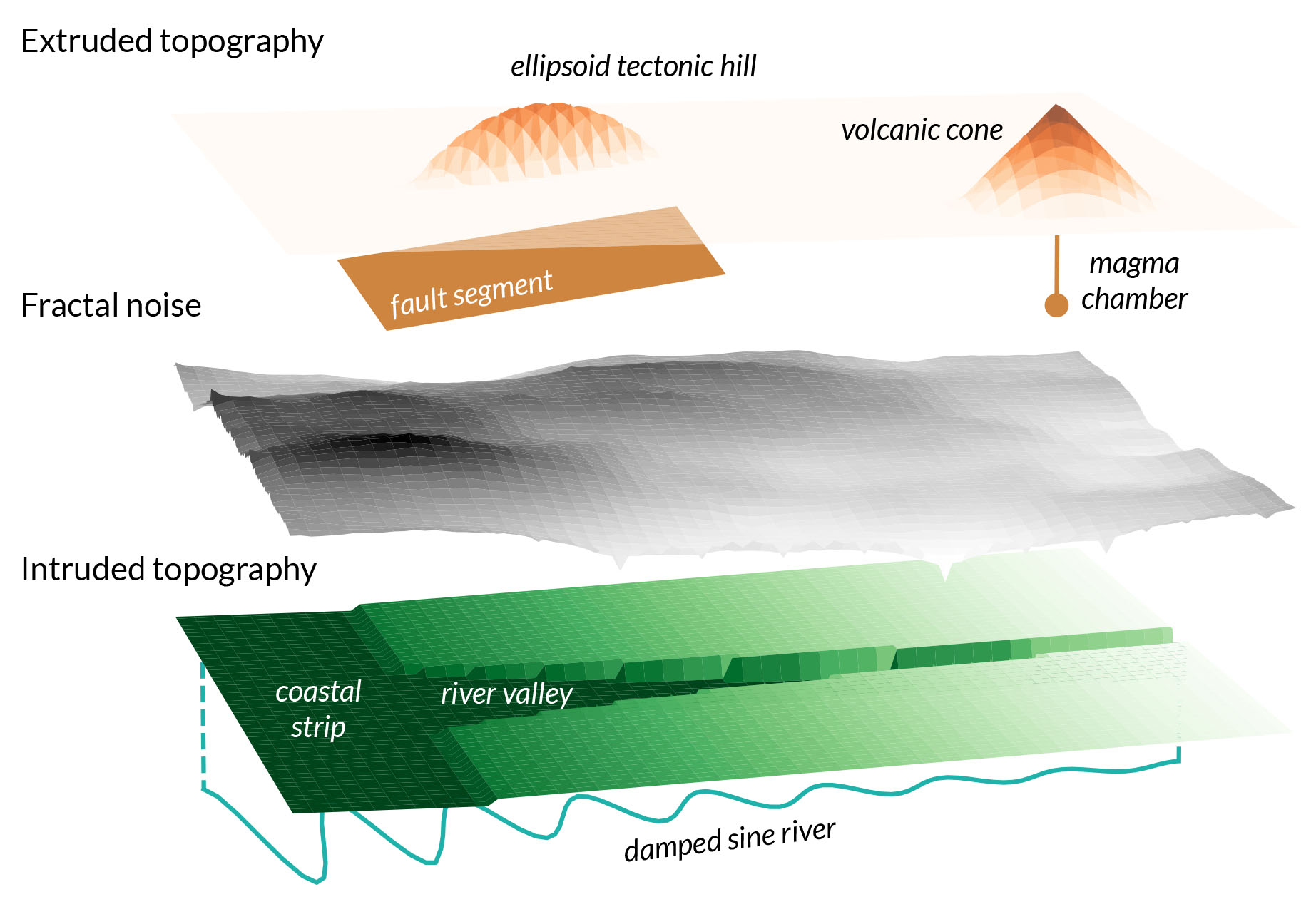
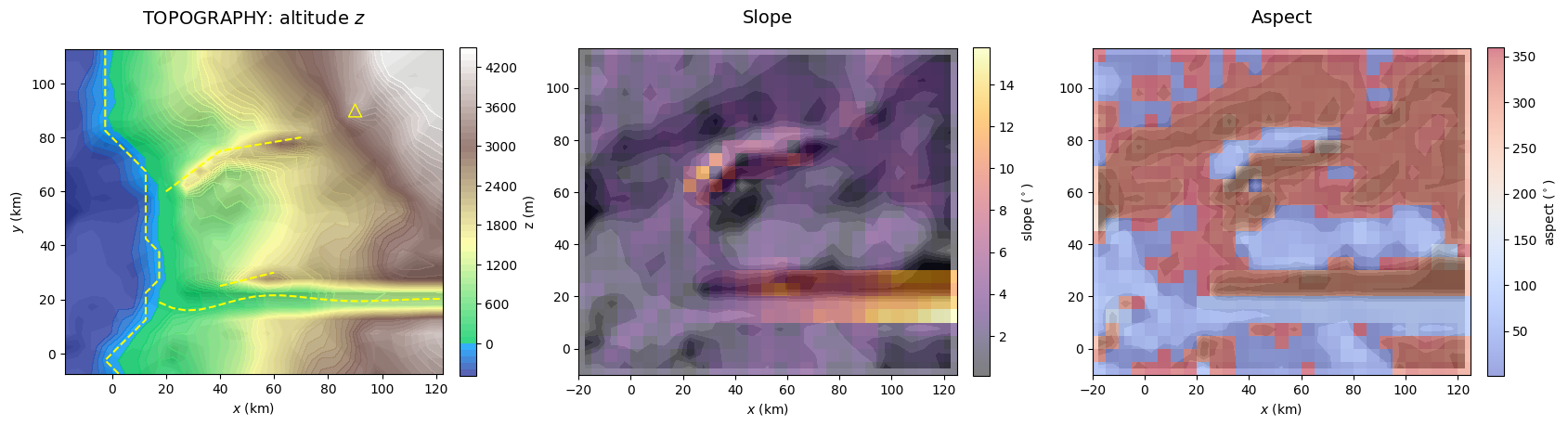
• Topography (topoLayer): Represented as the elevation \(z\) (m), the generic topography is defined by a west-dipping slope and a fractal dimension between 2 and 3. Environmental objects associated with peril sources modify the topography through intrusion and extrusion rules. The overall process, illustrated in Figure 2, combines methods from solid geometry and morphometry. Further details can be found in Mignan (2022). The main properties of the topography layer include terrain slope (\(^\circ\)) and aspect (\(^\circ\)).

Fig. 2. Construction of the topography layer following rules of solid geometry and morphometry, illustrating the combination of geometric primitives and terrain metrics. Redrawn from Mignan (2022:fig.2).

• Atmosphere (atmoLayer): Characterised by the mean near-surface air temperature \(T(z)\) function of the latitude and month of the year, based on the Energy Balance Climate Model (EBCM) of North et al. (1981). Properties include the freezing level \(z_{freeze}\) and the tropopause altitude \(z_{tropopause}\).

• Soil (soilLayer): Characterised by the soil thickness, \(h\) (m), which is initially spatially uniform. It can later vary through mass movement processes (using the landslide cellular automaton (CA) introduced in the next tutorial) or by a simpler rule applied here: \(h = 0\) (i.e., scarp) if the soil is unstable at \((x,y)\). Other soil properties remain fixed parameters at this stage. A key property of the soil layer is the factor of safety, \(F_S\), which indicates whether the soil is stable, critical, or unstable.

• Natural land (natLandLayer): Defined by the state \(S\), with \(S=-1\) for water, \(S=0\) for grassland, and \(S=1\) for forest. These classes represent the pre-urbanised land cover. All grid locations \((x,y)\) are considered forested except those above an elevation-dependent tree line (grassland), or below sea level (\(z = 0\)) and along river channels (water).

• Urban (urbLandLayer): Represents the built environment, where the state \(S\) overwrites the natural land classification: \(S = 2\) for housing, \(S = 3\) for industrial, and \(S = 4\) for commercial areas. The city is generated using a hybrid model that combines a simplified version of the SLEUTH city growth CA (Clarke et al., 1997; Candau, 2002), a road network CA (Koenig & Bauriedel, 2009), and a land-use transformation function (White et al., 1997) (Fig. 3; see Mignan (2024) for details). A key property of the urban-land layer is the asset value per pixel, which serves as the exposure component in the subsequent loss assessment tutorial.

  • Rural (optional): Converts eligible natural land cells to agricultural use (crops) according to spatial growth suitability criteria, with state \(S = 5\) representing wheat and \(S = 6\) representing maize.

Fig. 3. A simplified version of the Slope, Land use, Exclusion, Urban, Transportation, and Hill-shade (SLEUTH) model of urban growth (Clarke et al., 1997; Candau, 2002). Redrawn from Mignan (2024:box3.3).

Sections 1 and 2 detail the simulation of the virtual natural and technological environments, respectively (v1.1.1). A future Section 3, to be released in v1.1.2, will describe the socio-economic environment of the digital template.

## libraries ##
import numpy as np
import pandas as pd
import copy

import matplotlib.pyplot as plt
from matplotlib.patches import Polygon as MplPolygon

#import warnings
#warnings.filterwarnings('ignore')   # commented, try to remove all warnings

from GenMR import environment as GenMR_env
from GenMR import perils as GenMR_perils
from GenMR import utils as GenMR_utils

GenMR_utils.init_io()  # make folders /io and /fig if do not exist

1. Natural environment generation

The generic natural environment is constrained by a predominant west–east orientation, with a coastline located at x0. This configuration ensures that any water mass, when present, is systematically positioned on the western side of the grid (Fig. 1). By convention, rivers flow exclusively from east to west. This directional constraint simplifies the natural environment generator while still allowing it to represent a wide range of regional configurations.

1.1. Grid definition

All environmental layers are defined on the raster grid RasterGrid(). The default grid parameterisation gridPar (a dictionary) specifies an active domain of 100 × 100 km, with a reference north-south coastline fixed at x0 = 0 (i.e., \(z(x_0) = 0\)). A larger computational domain, bounded by (xmin, xmax, ymin, ymax), is included to account for potential boundary effects. The active box is thus defined as (xmin+xbuffer, xmax-xbuffer, ymin+ybuffer, ymax-ybuffer). The spatial resolution is determined by the pixel width w=0.1 km. Lower-resolution grids may be defined later for specific environmental processes. The parameter lat_deg specifies the latitude that drives the climate of the region. A lon_deg parameter will be added in a future release when a longitude reference becomes necessary for additional environmental processes.

gridPar = {'w': .1,
           'xmin': -20, 'x0': 0, 'xmax': 120, 'ymin': -10, 'ymax': 110,
           'xbuffer': 20, 'ybuffer': 10,
           'lat_deg': 30}

grid = GenMR_env.RasterGrid(gridPar)

1.2. Natural peril definition (for environmental objects)

Environmental layers can be influenced by specific environmental objects; this is notably the case for the first layer to be generated, the topography. In the context of a generic and parsimonious model, only essential objects are implemented. The environmental objects included here are restricted to those associated with the perils to be modelled in later stages.

Tab. 2. Characteristics of peril sources that generate environmental objects affecting the topography.

Peril	ID	Source	Environmental object	References
Earthquake	EQ	Fault of coordinates (x,y), width w_km, dip dig_deg, top depth z_km	Tectonic hill	Mignan (2022)
Fluvial flood	FF	River modelled as damped sine (riv_A_km, riv_lbd, riv_ome, riv_y0), with discharge Q_m3/s and implicit upstream catchment area A_km2	River valley	Mignan (2022)
Volcanic eruption	VE	Volcano of coordinates (x,y)	Conic volcanic edifice	Mignan (2022)

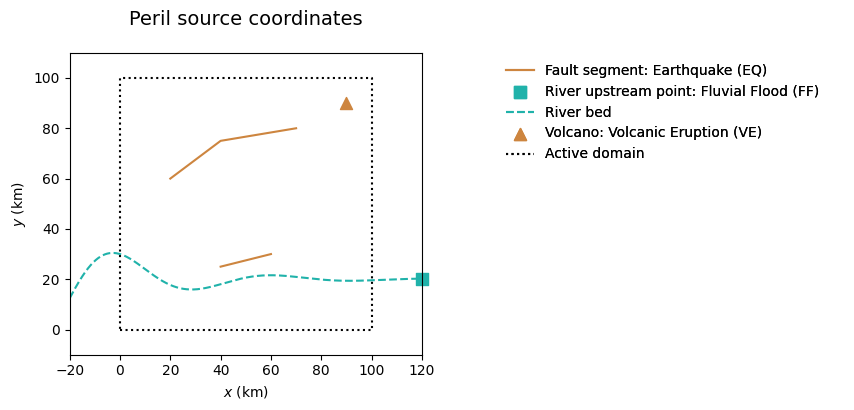
This configuration is parameterised using the dictionary srcPar. In this example, two faults, one river, and one volcano are defined. Additional perils will be introduced in the next tutorial. At this stage, only perils that can modify environmental layers are included.

srcPar = {
    'perils': ['EQ', 'FF', 'VE'],
    'EQ': {'object': 'fault',
        'x': [[20, 40, 70], [40, 60]],                                        # 2 faults (2 segments, 1 segment)
        'y': [[60, 75, 80], [25, 30]],
        'w_km': [5, 5], 'dip_deg': [45, 45],
        'z_km': [2, 2], 'mec': ['R', 'R'],                                    # only reverse R mechanism for now
        'bin_km': 1},                                                         # fault spatial resolution
    'FF': {'object': 'river',
        'riv_A_km': [10], 'riv_lbd': [.03], 'riv_ome': [.1], 'riv_y0': [20],  # y = A*exp(-lbd*x)*cos(ome*x)+y0
        'Q_m3/s': [100e3], 'A_km2': 100*100},
    'VE': {'object': 'volcano', 'x': [90], 'y': [90]},
}

src = GenMR_perils.Src(srcPar, grid)

GenMR_perils.plot_src(src)

1.3. Generating the topography, atmosphere, soil, and natural land layers

Environmental layers are defined as instance of classes EnvLayer_* (with * the layer ID; see Table 1). For this version of the digital template, parsimonious natural environment models with a minimal number of input parameters are favored for illustration purposes (at the cost of some simplifications). A few models will be mentioned below without going into any detail. Visit the GenMR_SCOR reference manual for an in-depth description.

The topography layer (parameterized in topoPar) is defined with the elevation \(z(x,y)\) as its main variable. It is constructed at a lower granularity with pixel width grid.w * lores_f. The process takes several successive steps:

• Background bg: Plane tilted westward with slope bg_tan(phi) anchored at \(z = 0\) at x0;

• Tectonic hill(s) th: Ellipsoid(s) with axes constrained by the 3D fault segment geometry (with centroid adjustable along the \(z\)-axis by th_Dz_km) extruding the topography;

• Volcano(s) vo: Cone(s) centered on the volcano coordinates with width vo_w_km and height vo_h_km extruding the topography;

• Fractal fr: Fractal noise (random seed fr_seed) with fractal dimension fr_Df and overall amplitude a fraction fr_eta of the background topography added to the topography. Uses the Diamond-square algorithm (Fournier et al., 1982). The coastline becomes irregular around x0 at this step;

• River valley(s) rv: Flat flood plain(s) tilted westward with slope rv_tan(phiWE) and N-S extend bound by the river exponential envelope intruding the topography (with angle rv_tan(phiNS) at the northern and southern boundaries). River channel(s) 2 N-S pixels wide for smooth flow and further intruded for normal channeled flow. Remnants of the original topography remain at a ratio rv_eta;

• Coastal strip cs: Coastal strip of width cs_w_km and slope cs_tan(phi) (< bg_tan(phi)) intruding the topography on the eastern side of the coastline. Remnants of the original topography remain at a ratio cs_eta.

At the end of the process, the layer is upscaled back to the default pixel width grid.w. Except for the background topography, all other alterations are optional (th, vo, fr, rv, cs true or false).

The atmospheric layer (paramerized in atmoPar) is defined with the near-surface air temperature \(T(z(x,y))\) as its main variable. The reference near-surface temperature \(T_0(z=0)\) is calculated from the Energy Balance Climate Model (EBCM) of North et al. (1981), which is function of gridPar['lat_deg'] and the considered month (see Appendix B1 for details). The temperature at any altitude is controlled by the lapse rate (lapse_rate_degC/km). Additional parameters pertaining to atmospheric pressure (p0_kPa) and moisture content (vz_subs_asc, eta_rain) are incorporated for use in climatological peril modeling in the following tutorial.

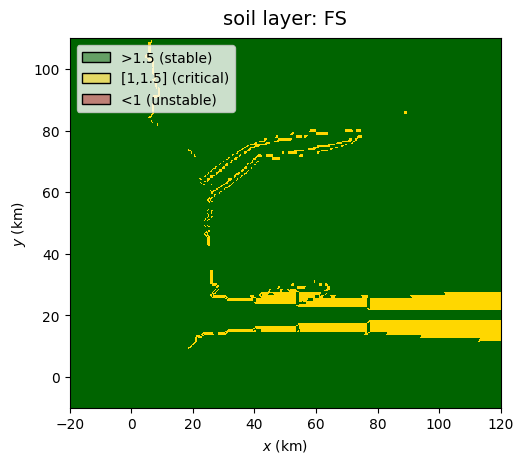
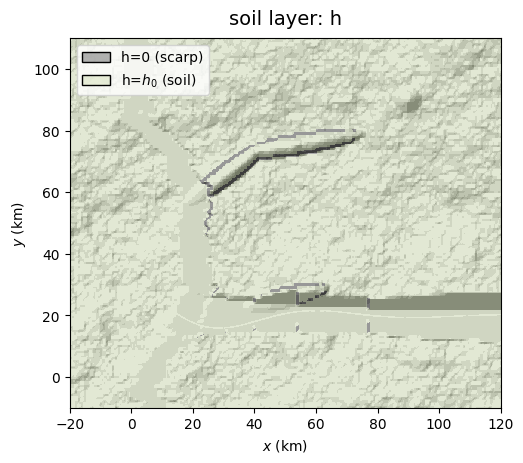
The soil layer (parameterized in soilPar) is defined by two main variables, the soil thickness \(h(x,y)\), initialised at constant value h0_m, and the water column depth \(h_w(x,y)\), initialized at hw0_m. Water content dynamics is controlled by the selected regime (moisture_regime: normal or stressed) and other parameters (theta_fc, porosity). Other soil parameters include the effective cohesion Ceff_Pa, effective friction angle phieff_deg and soil density rho_kg/m3 used for landslide modelling in Tutorial 2. \(h(x,y)\) is then updated with the method defined in corr (for correction). For simplicity, locations where the factor of safety is lower than 1 get \(h=0\) (method remove_unstable). \(h_w(x,y)\) will be allowed to vary in the next tutorial (during rainstorms).

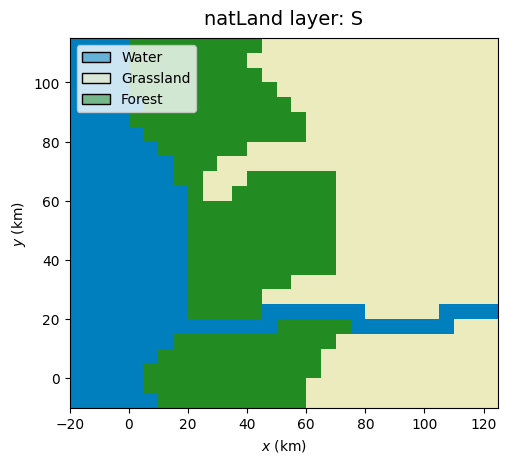
The natural land layer (parameterized in natLandPar) is defined by the state \(S(x,y)\), with \(S = -1\) (water) for \(z(x,y)<0\) (west of coastline) and at the coordinates of the river channel(s), \(S = 0\) (grassland) for \(z\) greater than ve_treeline_m, and \(S = 1\) (forest) otherwise (ve for vegetation). The land use state \(S\) will be further modified by urban and crop land classes in Section 2.

topoPar = {
    'lores_f': 10, 'bg_tan(phi)': 3/100,
    'th': True, 'th_Dz_km': -.5,
    'vo': True, 'vo_w_km': [9], 'vo_h_km': [1],
    'fr': True, 'fr_Df': 2.6, 'fr_eta': .5, 'fr_seed': 1,
    'rv': True, 'rv_tan(phiWE)': [1/1000], 'rv_tan(phiNS)': [1/2], 'rv_eta': .1,
    'cs': True, 'cs_w_km': 10, 'cs_tan(phi)': 1/1000, 'cs_eta': .1,
    'plt_zmin_m': -500, 'plt_zmax_m': 4500,
    'calc_d2coastline': True,    # must be True if 'urbLandPar['crops'] = True' & to define industrialZones
    'calc_d2river': True         # must be True to define industrialZones
}

atmoPar = {
    'lat_deg': gridPar['lat_deg'],
    'lapse_rate_degC/km': 6.5,   # rate at which temperature falls with altitude z
    'p0_kPa': 101.3,             # standard mean sea-level atmospheric pressure (International Standard Atmosphere)
    'vz_subs_asc': [-1e-3, 1.],  # large-scale vertical velocity (m/s), w < 0: subside (anticyclone)
                                 #                           w > 0: ascent (cyclone), high in strong convection
    'eta_rain': .5               # rain efficiency factor (NB: increase to .8 for organized systems?)
}

soilPar = {'h0_m': 10,           # soil depth
           'moisture_regime': 'normal',                             # 'normal' or 'stressed'
           'hw0_m': 0,           # soil moisture as water column (updated during soil water storage calculations)
           'theta_fc': .3,       # field_capacity: water content after excess-water has drained away
           'porosity': .5,
           'Ceff_Pa': 20e3, 'phieff_deg': 27, 'rho_kg/m3': 2650,    # for landslides (LS)
           'corr': 'remove_unstable'}
soilPar['hw_max_m'] = soilPar['porosity'] * soilPar['h0_m']         # maximum water content before waterlogging
soilPar['hw_fc_m'] = soilPar['theta_fc'] * soilPar['h0_m']          # stable maximum water content
if soilPar['moisture_regime'] == 'normal':
    soilPar['hw0_m'] = .7 * soilPar['hw_fc_m']
elif soilPar['moisture_regime'] == 'stressed':                      # increased drought (Dr) likelihood
    soilPar['hw0_m'] = .3 * soilPar['hw_fc_m']
# WARNING non 0 value fo hw0_m still to test...
    
natLandPar = {'ve_treeline_m': 2000}

We build all the natural environmental layers at once. Notice that each new layer builds upon the characteristics of the previous one(s):

grid = GenMR_env.RasterGrid(gridPar)
topoLayer = GenMR_env.EnvLayer_topo(src, topoPar)
atmoLayer = GenMR_env.EnvLayer_atmo(topoLayer, atmoPar)
soilLayer = GenMR_env.EnvLayer_soil(topoLayer, soilPar)
natLandLayer = GenMR_env.EnvLayer_natLand(soilLayer, natLandPar)

# peril sources and environmental layers saved in folder 'io/'
GenMR_utils.save_class2pickle(src, filename = 'src')
GenMR_utils.save_class2pickle(topoLayer, filename = 'envLayer_topo')
GenMR_utils.save_class2pickle(atmoLayer, filename = 'envLayer_atmo')
GenMR_utils.save_class2pickle(soilLayer, filename = 'envLayer_soil')
GenMR_utils.save_class2pickle(natLandLayer, filename = 'envLayer_natLand')

Calculating distance to coastline: 100%|████| 1401/1401 [00:38<00:00, 36.41it/s]
Calculating distance to river: 100%|████████| 1401/1401 [00:34<00:00, 40.55it/s]

1.4. Environmental layer variable & properties plotting

In addition to the variables that define their state, environmental layers include built-in derived properties (Tab. 1, A1). The function plot_EnvLayers() visualizes the primary variable(s) of each listed environmental layer along with selected key properties. When the argument file_ext is defined as jpg, pdf or some other format accepted by matplotlib.pyplot.savefig(), a file is created in the folder 'figs/'):

GenMR_env.plot_EnvLayers([topoLayer, atmoLayer, soilLayer, natLandLayer], file_ext = 'jpg')

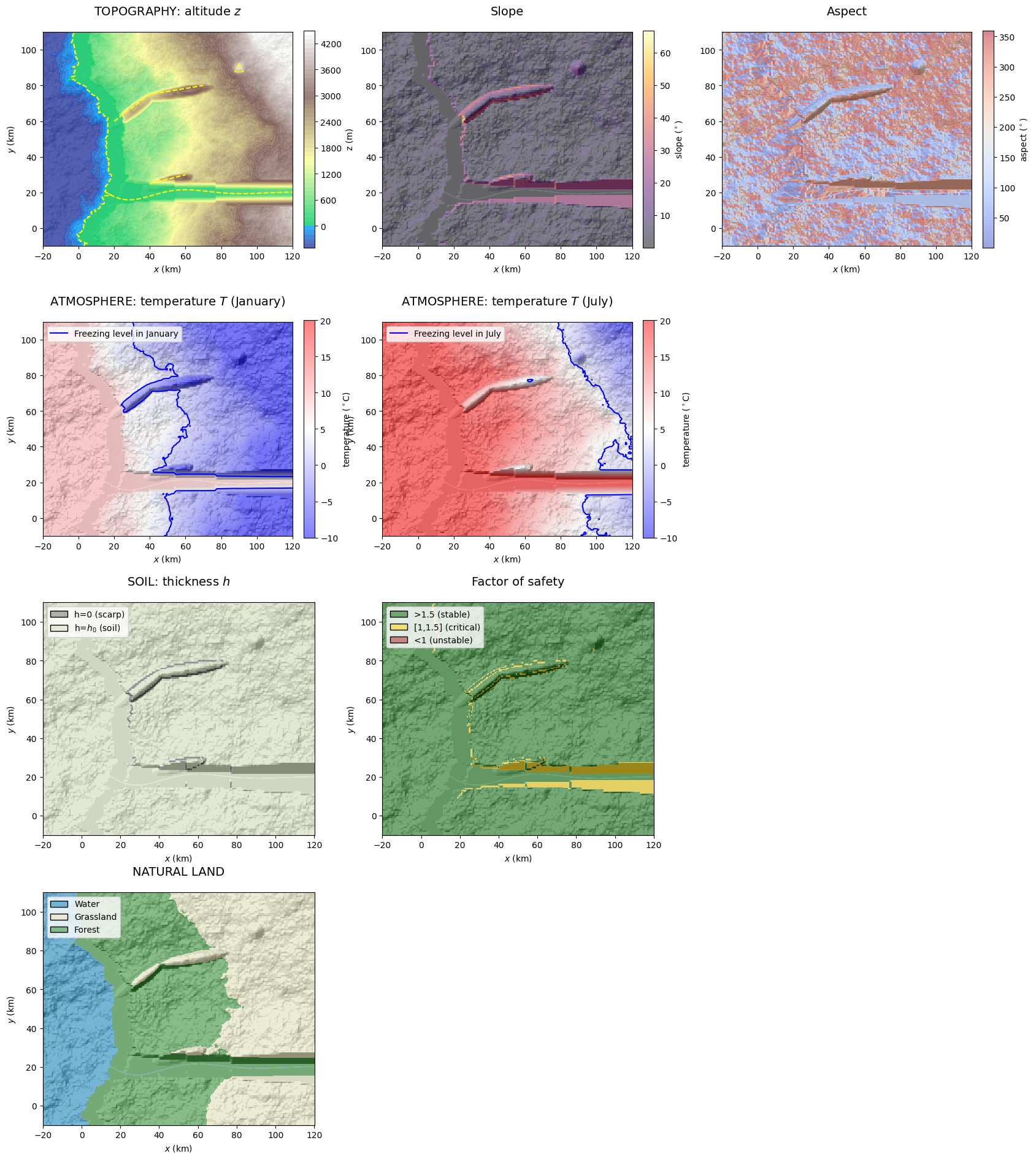
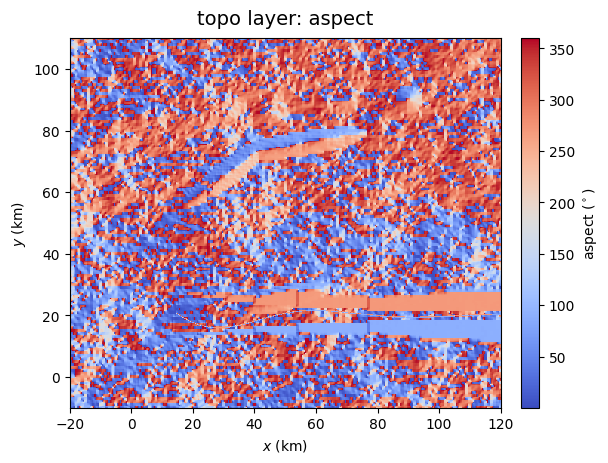
The function plot_EnvLayer_attr() plots individual variables and properties from environmental layers. If the elevation is given in the argument hillshading_z, hill shading is added in the background.

GenMR_env.plot_EnvLayer_attr(topoLayer, 'aspect', file_ext = 'jpg')
GenMR_env.plot_EnvLayer_attr(soilLayer, 'FS')
GenMR_env.plot_EnvLayer_attr(soilLayer, 'h', hillshading_z = topoLayer.z)

2. Technological environment generation

The technological system encompasses all human-made artifacts and engineered environments. This includes the built environment, critical infrastructure systems (such as transportation networks and energy generation and distribution), and agricultural production systems (i.e., crops) in rural areas. Goods and services delivered through businesses are classified within the socio-economic system (future Section 3).

2.1. Generating the urban land layer (incl. crops)

2.1.1. Generating the urban lan & intertwined road network object

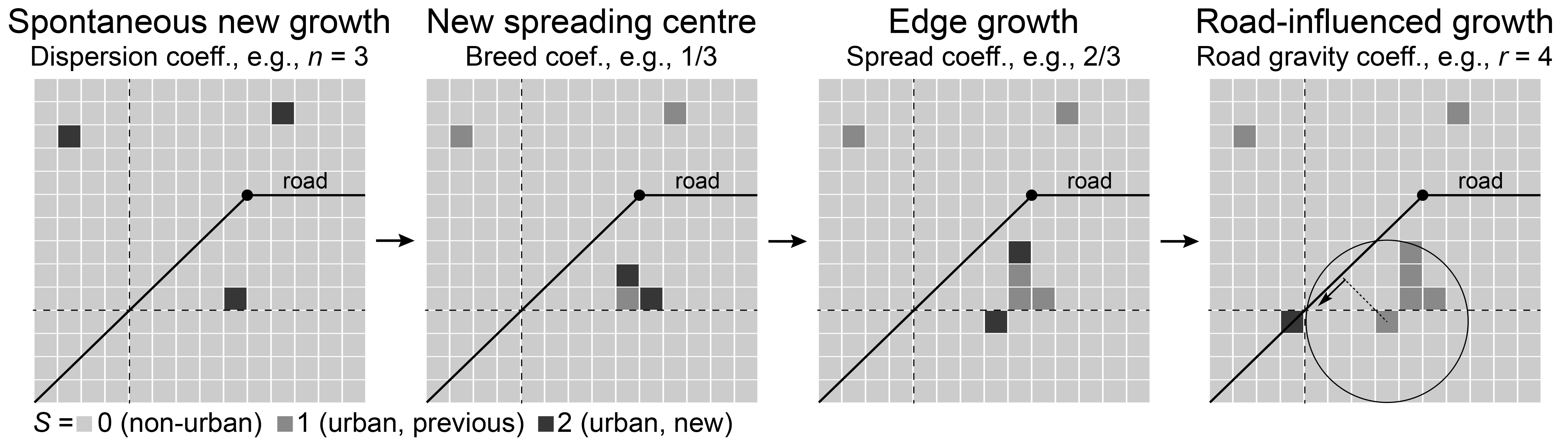
The urban land layer (parameterized in urbLandPar) updates the natural land layer by urbanising grid pixels with new states \(S = 2\) for residential, \(S = 3\) for industrial and \(S = 4\) for commercial. The city nucleates at city_seed\((x,y)\) and grows for a period of city_yrs years by following the main rules of the SLEUTH cellular automaton (Clarke et al., 1997; Candau et al., 2002; Candau, 2002) parameterized by SLEUTH_*. Each year, the city develops constrained on the road network configuration (an environmental object in the digital template) that grows in parallel to the city, and which is also based on a cellular automaton (Koenig & Bauriedel, 2009) with parameters road_* in the dictionary urbLandPar. After each built per simulation-year, built grid pixels get their state \(S\) following the land-use transformation function of White et al. (1997:tab.1). The full description of this hybrid city-generator will be given in a future article (Mignan, in prep.; see Mignan, 2024:boxes 3.1-3.3 for a summary).

On the SLEUTH model: Note that the SLEUTH algorithm used for GenMR_SCOR was developed from the modelling instructions provided in Clarke et al. (1997) and Candau (2002) to gain knowledge on the general process of city growth. It is therefore likely that the code differs in several ways from the official SLEUTH urban growth model. Consider using sleuth-automation for any dedicated SLEUTH model use. The class GenMR.environment.EnvLayer_landUrb() includes a road network cellular automaton within the SLEUTH loop and adds the land use transformation function of White et al. (1997) instead of the SLEUTH Deltatron at the end of each year-run.

Depending on the value given to city_yrs, city generation can take several minutes or more (up to approximately 30 minutes for a 100-year build-out). To accelerate the process, users may bypass regeneration and directly load a previously saved urbLandLayer class instance by setting file_urbLandLayer = 'envLayer_urbLand.pkl' below, provided that the file already exists.

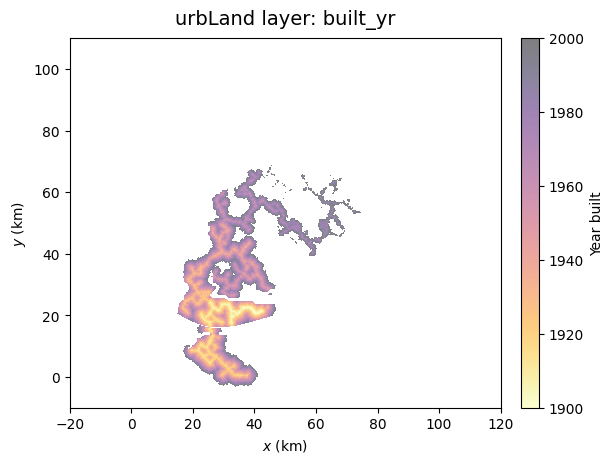
For economic loss assessment in the following tutorials, additional properties are defined for each building block at the resolution of grid.w. Four generic building materials (bldg_type) are considered: Wood (W) and Masonry (M) for residential, Reinforced Concrete (RC) for commercial, and Steel (S) for industry. The value of each building block (bldg_blockValue) is estimated as a function of GDP per capita (GDP_percapita_EUR) using a power-law relationship \(C = c_1\)GDP\(^{c_2}\) where \(C\) is the building construction cost (EUR/m\(^2\)) and GDP the per-capita GDP. Empirical parameters \(c_1\) and \(c_2\) are obtained from Huizinga et al. (2017:tab.3.25) for each occupancy type. The building block value bldg_blockValue is then approximated as \(C\) multiplied by the cell area (corrected by the factor ResComInd_Aratio) and the number of stories (bldg_Nstories).

2.1.2. Modelling crops

Two types of crops are modelled (wheat and maize), based on a temperature-based crop suitability index calculated from monthly near-surface air temperature and on other physical constraints defined by threshold crop_* in urbLandPar (see function crop_T_suitability()).

#file_urbLandLayer = ''           # run the city growth model if '' provided
file_urbLandLayer = 'envLayer_urbLand.pkl'    # if already exists

urbLandPar = {
    'lores_f': 10, 'rdm_seed': 1,     # 
    'city_seed': [40.5,20.5],         # coordinates of city seed centre (put near river as historical centre)
    'city_yr0': 1900,                 # year of settlement creation
    'city_yrs': 100,                  # number of years for urban growth from seed
    'SLEUTH_maxslope': 22,            # cannot build above (°) - Candau & Rasmussen (2000:2)
    'SLEUTH_disp': 10,                # dispersion coefficient
    'SLEUTH_breed': 50,               # breed coefficient
    'SLEUTH_spread': 20,              # spread coefficient
    'SLEUTH_slope': 90,
    'SLEUTH_roadg': 4,                # road gravity
    'road_growth': 2,                 # number of road network nodes generated per year
    'road_Rmax': 3,                   # max. radius in terms of number of perpendicular cells
    'road_maxslope': 10,              # cannot build above (degree)
    'road_X': 6,                      # 
    # building char. #
    'ResIndCom_yr_lowrise_end': [1970, 1970, 1970],  # historic low-rise period end (started in city_yr0)
    'ResIndCom_lowrise_max': [4, 2, 6],              # max. number of stories in low-rise buildings
    'ResIndCom_highrise_max': [10, 3, 30],           # max. number of stories in high-rise buildings
    'ResIndCom_mix_pr_high': [.2, .3, .2],           # mixed regime probability of high-rise
    'bldg_RES_wood2brick': .6,        # ratio of number of RES. blocks made of wood relative to bricks (masonry)
    'ResIndCom_Aratio': [.5, .6, .6], # fraction of grid cell that is actually built
    'GPD_percapita_EUR': 40e3,        # GDP per capita (USD) used to estimate construction cost for res, com, ind.
    # crop char. #
    'crops': True,                    # if True, crop classes modelled (wheat and maize hardcoded)
    'crop_slope_max': 3.,             # maximum slope (°)
    'crop_z_max': 1500.,              # maximum altitude (m)
    'crop_h_min': .5,                 # minimum soil depth (m)
    'crop_dcoast_min': 5.,            # minimum distance from coastline, i.e., saltwater intrusion limit (km)
    'crop_Tindex_min': 0.             # crop only generated above Tindex_min temperature suitability (0-1)
}

GenMR_utils.save_dict2json(urbLandPar, filename = 'par_urbLand')

if len(file_urbLandLayer) != 0:
    urbLandLayer = GenMR_utils.load_pickle2class('/io/' + file_urbLandLayer)
    print('... urbLandLayer class instance loaded')
else:
    urbLandLayer = GenMR_env.EnvLayer_urbLand(natLandLayer, atmoLayer, urbLandPar)
    urbLandLayer.generate()
    # get cached industrialZones before saving
    industrialZones = urbLandLayer.industrialZones
    GenMR_utils.save_class2pickle(urbLandLayer, filename = 'envLayer_urbLand')

... urbLandLayer class instance loaded

2.2. Generating the energy infrastructure

IN CONSTRUCTION

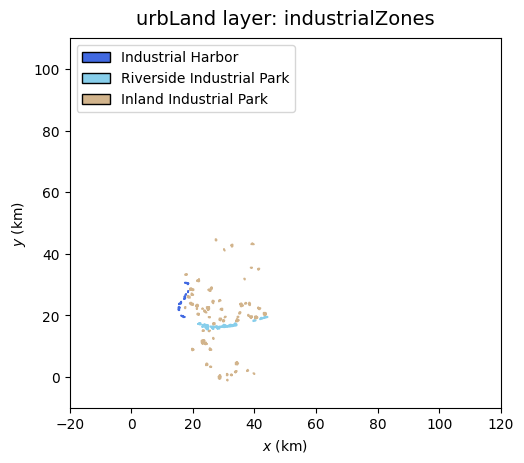
• Refinery: Identified as a critical infrastructure point situated at the centroid of the largest industrial harbor zone (industrialZones = 'industrial harbor') and a potential source of industrial explosions in Tutorial 2.

• Power grid: TO ADD

energyPar = {
    'rdm_seed': None
}

energyLayer = GenMR_env.EnvLayer_energyCI(urbLandLayer, energyPar)
GenMR_utils.save_class2pickle(energyLayer, filename = 'envLayer_energyCI')

2.3. Environmental layer properties

We will again use the function plot_EnvLayer() to display the environmental layer main attributes and other properties. For a landUrbLayer class instance, the main attribute is the land-use state \(S\). Properties are listed in Table A1 and can be plotted individually by using plot_EnvLayer_attr() (e.g., 'built_yr', 'industrialZones').

#GenMR_env.plot_EnvLayers([urbLandLayer], file_ext = 'jpg')
GenMR_env.plot_EnvLayers([topoLayer, soilLayer, urbLandLayer], file_ext = 'jpg')

GenMR_env.plot_EnvLayer_attr(urbLandLayer, 'built_yr')
GenMR_env.plot_EnvLayer_attr(urbLandLayer, 'industrialZones')

# tmp - show refinery location on map

fig, ax = plt.subplots(1,1, figsize=(20,10))

coast_x, coast_y = topoLayer.coastline_coord
riv_x, riv_y, _, _ = topoLayer.river_coord

ax.contourf(grid.xx, grid.yy, GenMR_env.ls.hillshade(topoLayer.z, vert_exag=.1), cmap='gray')
ax.plot(coast_x, coast_y, color = 'yellow', linestyle = 'dashed')
ax.plot(riv_x, riv_y, color = 'yellow', linestyle = 'dashed')
for poly in urbLandLayer.industrialZones:
    patch = MplPolygon(
            poly['vertices'],
            closed=True,
            facecolor = GenMR_utils.col_industrialZone.get(poly['zone_type'], 'gray'),
            edgecolor='black',
            alpha=1.,
            linewidth=.5
    )
    ax.add_patch(patch)

cx, cy = energyLayer.CI_refinery.centroid
ax.scatter(cx, cy, color = 'darkorange', marker = '+', s = 400, linewidth = 4, label = 'Refinery (CI)')
scatter_handles, scatter_labels = ax.get_legend_handles_labels()

all_handles = GenMR_env.lgd_industrialZone + scatter_handles
all_labels  = [h.get_label() for h in GenMR_env.lgd_industrialZone] + scatter_labels
ax.legend(all_handles, all_labels, loc='upper left')

ax.set_xlabel('$x$ (km)')
ax.set_ylabel('$y$ (km)')
ax.set_xlim(10,50)
ax.set_ylim(10,40)
ax.set_title('Industrial zones & critical infrastructures', size = 14, pad = 20)
ax.set_aspect(1);

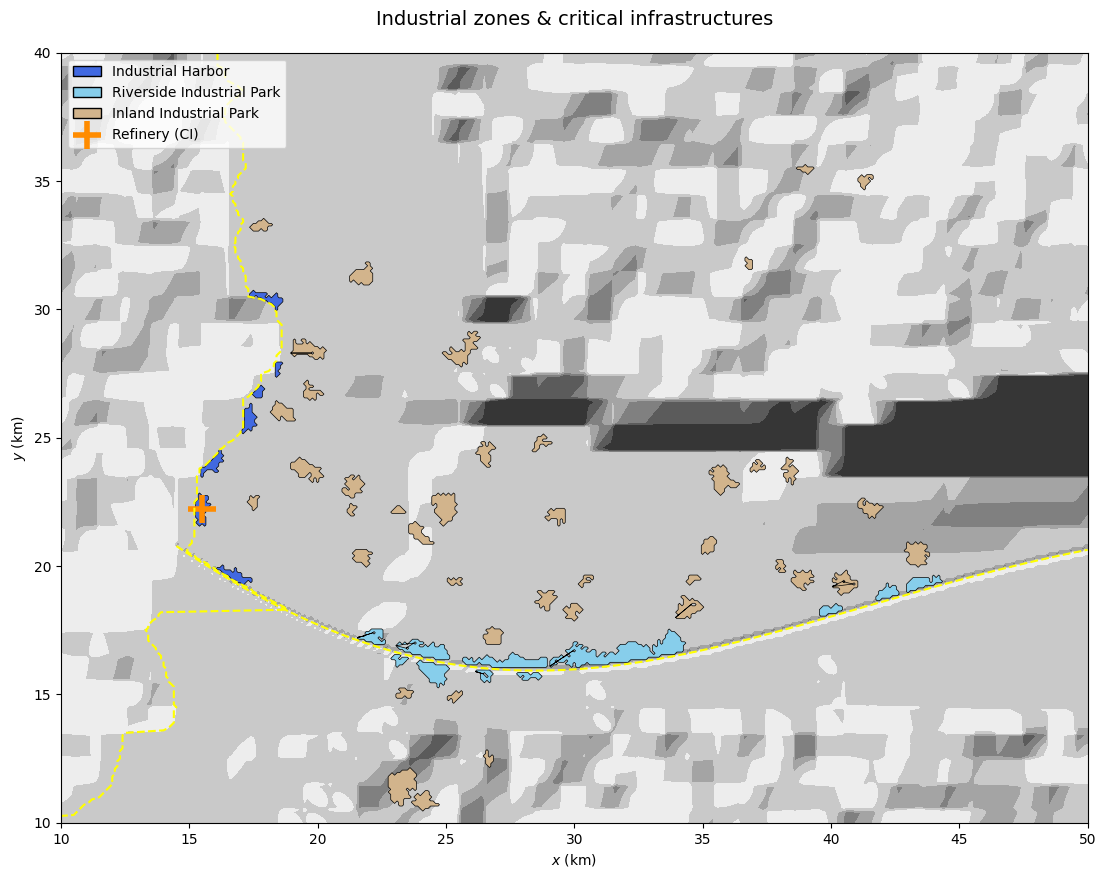
# TO DO for v1.1.2: add economic zones for BI events

3. Socio-economic environment generation

TO DO

References

• Candau JT (2002), Temporal calibration sensitivity of the SLEUTH urban growth model. Master Thesis, University of California Santa Barbara, 130 pp.

• Clarke KC, Hoppen S, Gaydos L (1997), A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area. Environment and Planning B: Planning and Design, 24, 247-261.

• Fournier A, Fussell D, Carpenter L (1982), Computer Rendering of Stochastic Models. Communications of the ACM, 25, 371–384.

• Huizinga J, de Moel H, Szewczyk W (2017), Global Flood Depth-Damage Functions. Methodology and the Database with Guidelines. JRC Technical Reports. EUR 28552 EN

• Koenig R, Bauriedel C (2009), Generating settlement structures: a method for urban planning and analysis supported by cellular automata. Environment and Planning B: Planning and Design, 36, 602-624.

• Mignan A (2022), A Digital Template for the Generic Multi-Risk (GenMR) Framework: A Virtual Natural Environment. International Journal of Environmental Research and Public Health, 19 (23), 16097, doi: 10.3390/ijerph192316097

• Mignan A (2024), Introduction to Catastrophe Risk Modelling - A Physics-based Approach. Cambridge University Press, doi: 10.1017/9781009437370

• Morgan-Wall T (2022), rayshader: Create Maps and Visualize Data in 2D and 3D. https://www.rayshader.com.

• North et al. (1981), Energy Balance Climate Models. Rev. Geophys. Space Phys. 19(1), 91-121.

• White R, Engelen G, Uljee I (1997), The use of constrained cellular automata for high-resolution modelling of urban land-use dynamics. Environment and Planning B: Planning and Design, 24, 323-343.

Appendix

A. Attributes & properties of environmental layers

Tab. A1. Full list of attributes and properties in environmental layers EnvLayer_ID.

Layer class ID	Variable\(^*\) or property	ID	Description
topo	Elevation\(^*\)	z	Surface altitude (m)
topo	Object coordinates	coastline_coord	Coordinates of the coastline
topo	Object coordinates	river_coord	Coordinates of the river(s)
topo	Slope	slope	Terrain slope (\(^\circ\))
topo	Aspect	aspect	Azimuth that the terrain surface faces (\(^\circ\))
atmo	Near-surface air temperature\(^*\)	T	Mean value (\(^\circ\)C) at \(z(x,y)\) per month
atmo	Tropopause	z_tropopause	Altitude (km) of tropopause
atmo	Freezing level	z_freezinglevel	Altitude (km) of 0\(^\circ\)C, monthly
soil	Soil thickness\(^*\)	h	(m)
soil	Water column\(^*\)	hw	Water height in soil (m)
soil	Factor of safety value	FS_value	Describes the stability level of the soil
soil	Factor of safety state	FS_state	stable (\(=0\)), critical (\(=1\)), unstable (\(=2\))
soil	Wetness	wetness	Ratio between hw and h
natLand	Land use class\(^*\)	S	Water (\(=-1\)), grassland (\(=0\)), forest (\(=1\))
natLand	Water column	hW	Water level above soil (in river)
urbLand	Land use class\(^*\)	S	Occupancy: residential (\(=2\)), industrial (\(=3\)), commercial (\(=4\))
			Crops: wheat (\(=5\)), maize (\(=6\))
urbLand	Built year	built_yr	Year in which the city block has been built
urbLand	Building type	bldg_type	Wood (W), masonry (M), reinforced concrete (RC), steel (S)
urbLand	Building roof pitch	bldg_roofpitch	Low (L), medium (M), high (H)
urbLand	Number of stories	bldg_Nstories	Number of stories per building block
urbLand	Building block value	bldg_blockValue	Construction cost of entire block (EUR)
urbLand	Industrial zone type	industrialZones	Harbor, riverside, inland zone polygons
urbLand	Object coordinates	roadNet_coord	Coordinates of the road network
energyCI	Object coordinates	CI_refinery	Refinery coordinates

A.1 A note on environmental layer downscaling

Different environmental processes may occur at different scales. The default resolution is defined by the pixel width grid.w, which represents the finest one possible for environmental layers. A grid class instance can be downscaled with the function downscale_RasterGrid(). This was for example used to generate the topography (in EnvLayer_topo()). Another process defined at lower resolution will be the road network in Section 2 which will required downscaled terrain slope and water mask as inputs. Different pooling methods (minimum, mean or maximum) are available in function pooling(). This is illustrated below with the resolution reduced by a factor f = 50 to emphasize the impact on the layers.

f = 50
grid_downscaled = GenMR_env.downscale_RasterGrid(grid, f, appl = 'pooling')
topoLayer_downscaled = copy.deepcopy(topoLayer)
topoLayer_downscaled.grid = grid_downscaled
topoLayer_downscaled.z = GenMR_utils.pooling(topoLayer.z, f, method = 'mean')             # mean-pooling example

GenMR_env.plot_EnvLayers([topoLayer_downscaled])    # notice that properties are automatically recomputed

natLandLayer_downscaled = copy.deepcopy(natLandLayer)
natLandLayer_downscaled.grid = grid_downscaled
natLandLayer_downscaled.S = GenMR_utils.pooling(natLandLayer.S, f, method = 'min')        # min-pooling example

GenMR_env.plot_EnvLayer_attr(natLandLayer_downscaled, 'S')

B. Underlying physical processes

B.1. Atmospheric layer: Temperature

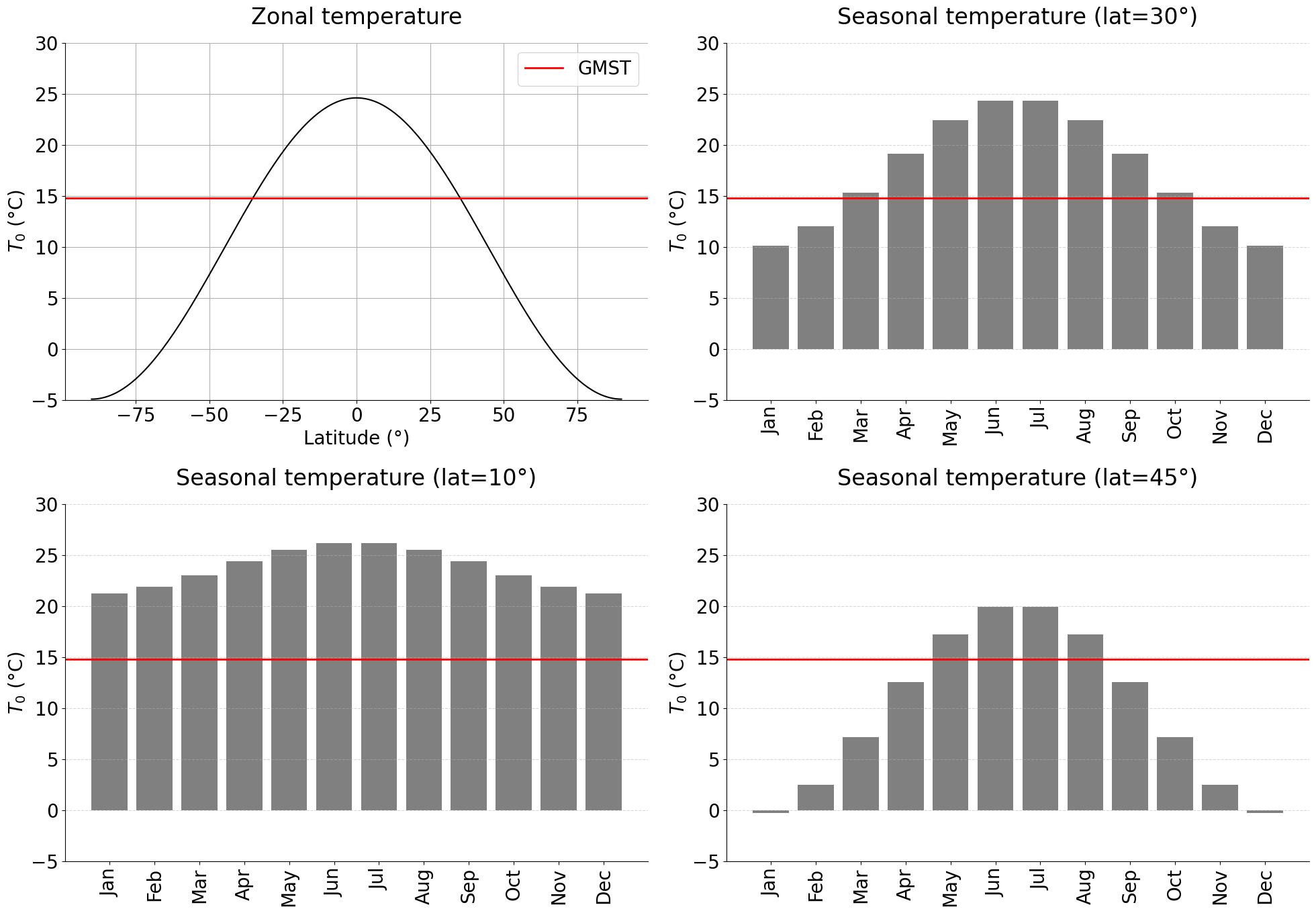
The reference near-surface air temperature T0 is calculated using the Energy Balance Climate Model (EBCM) of North et al. (1981). The next cell shows how T0 depends on the latitude of the digital template and the month considered (see future Tutorial 3 for the implementation of seasonality in CAT modelling).

lat_low, lat_med, lat_hig = 10, 30, 45
lati = np.arange(-90,91)
moni = np.arange(12)+1

_, T0_zonal, GMST = GenMR_env.EnvLayer_atmo.calc_T0_EBCM(lati, np.nan)
print(f'Global mean surface temperature (GMST): {GMST}°C')
GMST_from_zonal = np.average(T0_zonal, weights = np.cos(np.radians(lati)))
print(f'Average zonal temperature = {GMST_from_zonal}°C (= GMST, validation value)')

T0_low, _, _ = GenMR_env.EnvLayer_atmo.calc_T0_EBCM(lat_low, moni)
T0_med, _, _ = GenMR_env.EnvLayer_atmo.calc_T0_EBCM(lat_med, moni)
T0_hig, _, _ = GenMR_env.EnvLayer_atmo.calc_T0_EBCM(lat_hig, moni)

plt.rcParams['font.size'] = '20'
fig, ax = plt.subplots(2,2, figsize = (20,14))
Tmin, Tmax = -5., 30.

ax[0,0].plot(lati, T0_zonal, color = 'black')
ax[0,0].axhline(GMST, color = 'red', linewidth = 2, label = 'GMST')
ax[0,0].set_xlabel('Latitude (°)')
ax[0,0].set_ylabel('$T_0$ (°C)')
ax[0,0].set_title('Zonal temperature', pad = 20)
ax[0,0].grid()
ax[0,0].legend()
ax[0,0].set_ylim(Tmin, Tmax)
ax[0,0].spines['right'].set_visible(False)
ax[0,0].spines['top'].set_visible(False)

ax[0,1].bar(moni, T0_med, color='grey')
ax[0,1].axhline(GMST, color = 'red', linewidth = 2)
ax[0,1].set_xticks(moni, GenMR_utils.month_labels_short, rotation=90)
ax[0,1].set_ylabel('$T_0$ (°C)')
ax[0,1].set_title(f'Seasonal temperature (lat={lat_med}°)', pad = 20)
ax[0,1].grid(axis='y', linestyle='dashed', alpha=.5)
ax[0,1].set_ylim(Tmin, Tmax)
ax[0,1].spines['right'].set_visible(False)
ax[0,1].spines['top'].set_visible(False)

ax[1,0].bar(moni, T0_low, color='grey')
ax[1,0].axhline(GMST, color = 'red', linewidth = 2)
ax[1,0].set_xticks(moni, GenMR_utils.month_labels_short, rotation=90)
ax[1,0].set_ylabel('$T_0$ (°C)')
ax[1,0].set_title(f'Seasonal temperature (lat={lat_low}°)', pad = 20)
ax[1,0].grid(axis='y', linestyle='dashed', alpha=.5)
ax[1,0].set_ylim(Tmin, Tmax)
ax[1,0].spines['right'].set_visible(False)
ax[1,0].spines['top'].set_visible(False)

ax[1,1].bar(moni, T0_hig, color='grey')
ax[1,1].axhline(GMST, color = 'red', linewidth = 2)
ax[1,1].set_xticks(moni, GenMR_utils.month_labels_short, rotation=90)
ax[1,1].set_ylabel('$T_0$ (°C)')
ax[1,1].set_title(f'Seasonal temperature (lat={lat_hig}°)', pad = 20)
ax[1,1].grid(axis='y', linestyle='dashed', alpha=.5)
ax[1,1].set_ylim(Tmin, Tmax)
ax[1,1].spines['right'].set_visible(False)
ax[1,1].spines['top'].set_visible(False)

fig.tight_layout();

Global mean surface temperature (GMST): 14.763157894736834°C
Average zonal temperature = 14.76365750942746°C (= GMST, validation value)